动态规划（二）

2021-01-02

动态规划（二）

再列举一些经典的动态规划习题。

1. 最长回文子串

这是LeetCode 第5号问题。给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

思路：dp[i][j]表示s[i:j]是否为一个回文串，可知i <= j,dp[i][i] = true，当s[i] == s[j]时，s[i:j]是否是一个回文串就由s[i+1:j-1]来决定了，当s[i]!=s[j]，这是s[i:j]一定不是回文串。由此可以写出状态转移方程。

注意：需要注意的是，写循环的时候很容易弄混内外循环，以下两种枚举方式都是可行的。

以字符串"babab"为例，图解两种枚举方式状态如何转移。

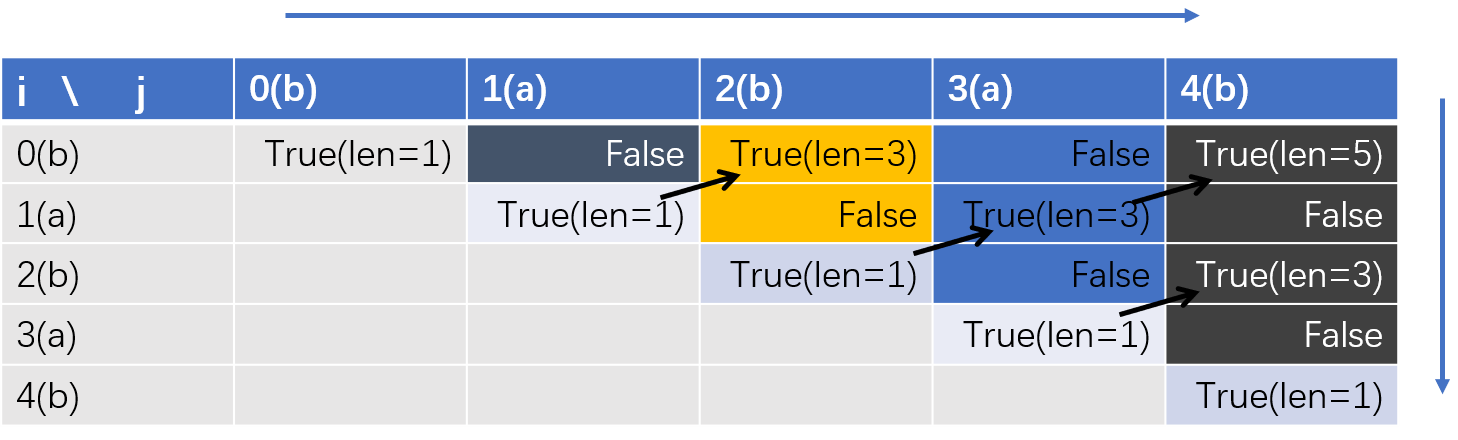
第一种方式(PPT作图真好用啊)。解释一下，以dp[0][4]为例，此时s[0] == s[4] == 'b'，这时需要判断dp[1][3]（即子串"aba"）是不是回文串，由于上一次循环已经得出dp[1][3]的结果是true，因此dp[0][4]结果也为true，并且长度为5（箭头表示这张表是从左到右，自上而下填写的）。

第一种

class Solution {
    public String longestPalindrome(String s) {
        char ch[] = s.toCharArray();
        int begin = 0, maxLen = 1, len = ch.length;
        boolean dp[][] = new boolean[len + 1][len + 1];
        for(int i = 0; i < len; i++){
            // 单个字母肯定是回文串
            dp[i][i] = true;
        }
        //dp[i][j] 表示s[i:j]是否为一个回文串 i <= j
        for(int j = 1; j < len; j++){//外层循环j
            for(int i = 0; i < j; i++){//内层循环i , 保证i <= j
                if(ch[i] != ch[j]){
                    dp[i][j] = false;
                }else{
                    if(j - i < 3){
                        //若长度为2，且两个字母相等，是回文串
                        dp[i][j] = true;
                    }else{
                        dp[i][j] = dp[i+1][j-1];
                    }
                }
                if(dp[i][j] && j - i + 1 > maxLen){
                    maxLen = j - i + 1;
                    begin = i;
                }

            }
        }
        return s.substring(begin, begin + maxLen );
    }
}

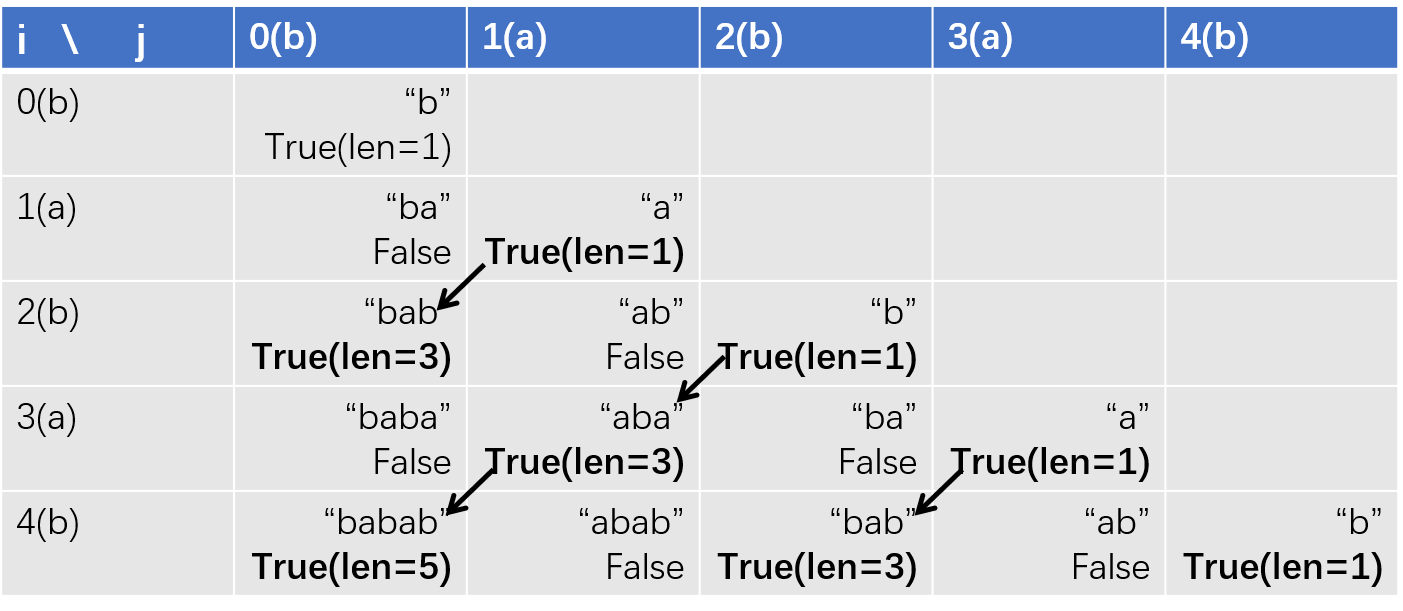
另一种递推方式。其实是在判断dp[j][i]是不是回文串。

方式2

代码如下：

class Solution {
    public String longestPalindrome(String s) {
        char ch[] = s.toCharArray();
        int begin = 0, maxLen = 1, len = ch.length;
        boolean dp[][] = new boolean[len + 1][len + 1];
        for(int i = 0; i < len; i++){
            // 单个字母肯定是回文串
            dp[i][i] = true;
        }
        for(int i = 0; i < len; i++){
            for(int j = 0; j < i; j++){
                if(ch[i] != ch[j]){
                    dp[i][j] = false;
                }else{
                    if(i - j < 3){
                        //若长度为2，且两个字母相等，是回文串
                        dp[i][j] = true;
                    }else{
                        dp[i][j] = dp[i-1][j+1];
                    }
                }
                if(dp[i][j] && i - j + 1 > maxLen){
                    maxLen = i - j + 1;
                    begin = j;
                }

            }
        }
        return s.substring(begin, begin + maxLen );
    }
}

2. 整数划分系列

2.1 整数划分1

将一个正整数划分为不大于自身的一系列正整数之和，给定$n$，求一共有多少种不同的划分方案。

整数划分

该题可以抽象为：给定一个容量为 n 的背包，有体积为1,2,3,4…,n的物品，求装满背包有多少种不同的装法。每个物品可以无限使用。与完全背包不同的是，完全背包最后求的是背包可以得到的最大价值，而本题求得是方案数。

首先先定义状态，和背包问题类似，我们可以定义dp[i][j]为使用前i个物品，装满容量为j的背包的方案数，所求答案即：dp[n][n]。对于每一个物品我们都可以选择装和不装；如果装入第i个物品，dp[i-1][j-i]，前提是j >= w[i] = i，如果不装，dp[i-1][j]，因此若j >= i,dp[i][j] = dp[i-1][j-i] + dp[i-1][j]，当j < w[i] = i，dp[i][j] = dp[i-1][j]，此时第i个物品不可用。注意初始化问题，体积为0时只有一种方案：啥也不装。

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1028

#include <iostream>
#include <cstring>
using namespace std;
const int mod = 1e9 + 9;
int m, n, dp[125][125];
int main()
{
    while(cin >> n){
        memset(dp,0,sizeof(dp));
        for(int i = 0; i <= n; i++){
            //初始化, 体积为0时只有一种方案：啥也不装
            dp[i][0] = 1;
        }
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= n; j++){
                if(j >= i){
                    dp[i][j] = dp[i-1][j] + dp[i][j-i];
                }else{
                    dp[i][j] = dp[i-1][j];
                }
            }
        }
        cout << dp[n][n] << endl;
    }
}

状态压缩：

#include <iostream>
#include <cstring>
using namespace std;
const int mod = 1e9 + 9;
long long t, n, dp[100005];
int main()
{
    cin >> t;
    while(t--){
        memset(dp,0,sizeof(dp));
        dp[0] = 1;
        cin >> n;
        for(int i = 1; i <= n; i++){
            for(int j = i; j <= n; j++){
                (dp[j] += dp[j - i]) %= mod;
            }
        }
        cout << dp[n] << endl;
    }
    return 0;
}

2.2 整数划分2

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。返回你可以获得的最大乘积。这是LeetCode 343号问题。

先这么想：设 f(n) 表示 n 拆分成至少2个整数的和的最大乘积。即

$f(n) = \max(1 * f(n - 1), 2 * f(n - 2), ... , (n-1) * f(1)$

，还有一种情况就是直接拆分成2个数的和，即$j*(i-j)$。可以看出这是递归，可以用自顶向下+记忆化解决，也可以自底向上通过递推解决。

class Solution {
    public int integerBreak(int n) {
        int dp[] = new int[n + 1];
        dp[1] = 1;
        for(int i = 2; i <= n; i++){
            for(int j = 1; j < i; j++){
                // 分为多个和 vs 直接分为两个和
                dp[i] = Math.max(Math.max(j * dp[i - j], j * (i - j)), dp[i]);
            }
        }
        return dp[n];
    }
}

注意：当n过于大时，这时就应该考虑采用数学方法求解了。

2.3 整数划分3

将整数n分成k份，且每份不能为空，例如：n=7，k=3，下面三种分法被认为是相同的。1,1,5; 1,5,1; 5,1,1;
问有多少种不同的分法。题目链接：https://vijos.org/p/1117

#include <iostream>

using namespace std;
int n,k,dp[205][10];
int main()
{
    cin >> n >> k;
    // n 划分为k份，有多少种分法？
    dp[0][0] = 1;
    for(int i = 1; i <= n; i++){
        // 任何一个数划分为1份只有1种分法
        dp[i][1] = 1;
    }
    // 状态转移方程
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= k; j++){
            if(i >= j){
                // i >= j 才讨论划分
                dp[i][j] = dp[i-j][j] + dp[i-1][j-1];
            }
        }
    }
    cout << dp[n][k] << endl;
    return 0;
}

3. 零钱兑换

3.1 零钱兑换 I

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。你可以认为每种硬币的数量是无限的。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/coin-change
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路分析:

同样的，这个问题也可以抽象成一个背包问题，背包容量为amount，物品价值为coins，状态dp[j]表示组成金额j时需要的最小硬币个数，dp[j] = min(dp[j], dp[j - coins[i]] + 1)，dp[j-coins[i]]表示使用第i个硬币来组成金额j，那么所需硬币个数就需要在dp[j-coins[i]]的基础上加1。

class Solution {
    public int coinChange(int[] coins, int amount) {
        int dp[] = new int[amount + 1];
        for (int i = 0; i <= amount; i++){
            dp[i] = amount + 1;
        }
        dp[0] = 0;
        for (int i = 0; i < coins.length; i++){
            for (int j = 1; j <= amount; j++){
                if (j - coins[i] >= 0)
                    dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
            }
        }
        return dp[amount] == amount + 1 ? -1 : dp[amount];
    }
}

3.2 零钱兑换 II

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。这是LeetCode第518号问题。

看懂了吗，这个题是不是和第一个整数划分问题一摸一样！！！

class Solution {
    public int change(int amount, int[] coins) {
        // 即使每个硬币可以无限使用，但是amount是有限的，对于coins[i],最多也就使用 round(amount/coins[i])
        int n = coins.length;
        int dp[][] = new int[n + 1][amount + 1];

        for(int i = 0; i <= n; i++){
            //初始化, 面额为0时只有一种方案
            dp[i][0] = 1;
        }
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= amount; j++){
                if(j - coins[i - 1] >= 0)
                    dp[i][j] = dp[i-1][j] + dp[i][j - coins[i-1]];
                else//j < coins[i-1] 当前硬币面额大于凑得数量不可用。
                    dp[i][j] = dp[i-1][j];
            }
        }
        return dp[n][amount];
    }
}

4. 最大正方形

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。LeetCode第221号问题（https://leetcode-cn.com/problems/maximal-square/）。

需要注意的是状态转移中取的是min，类似木桶原理，装水的多少由最短的那个木头决定。

class Solution {
    public int maximalSquare(char[][] matrix) {
        // dp[i][j]表示以i,j为右下角的含1的最大正方形的面积
        int row = matrix.length;
        if(row == 0){
            return 0;
        }
        int col = matrix[0].length;
        
        int dp[][] = new int[row + 1][col + 1];
        int maxn = Integer.MIN_VALUE;
        
        for(int i = 1; i <= row; i ++){
            for (int j = 1; j <= col; j ++){
                if(matrix[i-1][j-1] == '1')
                    dp[i][j] = Math.min(Math.min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1]) + 1;
                
                maxn = Math.max(dp[i][j], maxn);
            }
        }
        // 注意要求返回最大面积，dp表示的是边长
        return maxn * maxn;
    }
}

5. 交错字符串

给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错组成的。

即s3中属于s1的字符顺序构成s1，属于s2的字符顺序构成s2。

关于字符串的动态规划题还是挺有意思的。题解见下图：

给定：s1: “abc”,s2:”ead”,s3: ”aeabcd”

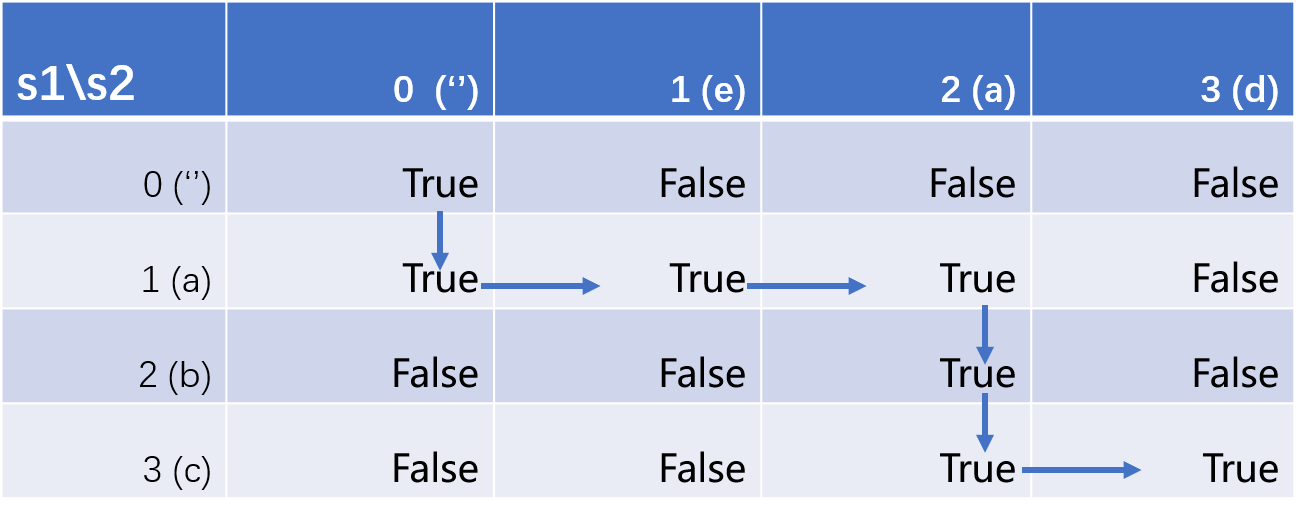
表格中$(i,j)$位置表示s1[:i-1],s2[:j-1]是否可以交错构成s3[:i+j-1]。

当 $i=1.j=1$ 为例，$(1,1)$ 表示s1第一个字符与s2第一个字符是否可以交错构成s3[:1]即前两个字符，进行判断：如果 s3[1] == s1[0]，那么当前状态由 dp[i-1][j]决定，即''与s2[0]是否可以构成s3[0]（转化为子问题），如果 s3[1] == s2[0]，那么转求dp[i][j-1]，即s1[0]与''是否可以构成s3[0]。可见s2第一个字符e与s3第二个字符相同，那么就判断空字符''与s1第一个字符a是否可以构成s3第一个字符a，明显可以，因此dp[1][1]为True。其余情况类同。

isInterleave

class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        char ch1[] = s1.toCharArray();
        char ch2[] = s2.toCharArray();
        char ch3[] = s3.toCharArray();
        int len1 = ch1.length, len2 = ch2.length;
        if (len1 + len2 != ch3.length){
            return false;
        }
        boolean dp[][] = new boolean[len1+1][len2+1];
        dp[0][0] = true;
        // 处理边界
        for (int i = 1; i <= len1; i++){
            dp[i][0] = ch1[i-1] == ch3[i-1] && dp[i-1][0];
        }
        for (int i = 1; i <= len2; i++){
            dp[0][i] = ch2[i-1] == ch3[i-1] && dp[0][i-1];
        }
        
        // dp[i][j] 表示 s1[0 - i-1] s2[0 - j-1] 是否可以交错构成 s3[0 : i + j - 1]
        for (int i = 1; i <= len1; i++){
            for (int j = 1; j <= len2; j++){
                dp[i][j] = dp[i-1][j] && ch1[i-1] == ch3[i+j-1] || dp[i][j-1] && ch2[j-1] == ch3[i+j-1];
            }
        }
        return dp[len1][len2];
    }
}