寻找重复数

2021-01-02

日常刷题记录。

1. 寻找重复数

给定一个包含 n + 1 个整数的数组 nums，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。假设只有一个重复的整数，找出这个重复的数。这是Leetcode 287号问题。

解法1：排序，然后看相邻元素是否是否相等

class Solution {
    public static int findDuplicate(int[] nums) { 
		Arrays.sort(nums);
        int ans = 0;
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] == nums[i - 1]) {
                ans = nums[i];
                break;
            }
        }
        return ans;
    }
}

解法2：hashmap统计次数或集合判重。

解法3：双指针

class Solution {
     // 数组中的值代表了索引，因为是1-n之间的数，数组包含n+1个数字，不会越界
     // nums[fast]->具体数值 以nums[fast]作为索引得到->nums[nums[fast]]
     // nums = [2,5,9,6,9,3,8,9,7,1] 构造成链表
     // 2->[9]->1->5->3->6->8->7->[9]->1->5->3...如果存在重复数字，有环存在，找到环的入口。
    public static int findDuplicate(int[] nums) { 
		int fast = 0, slow = 0;
        while (true) {
            fast = nums[nums[fast]];
            slow = nums[slow];
            // System.out.println("fast=" + fast + ",slow=" + slow);
            if (fast == slow)
                break;
        }
        int finder = 0;
        while (true) {
            finder = nums[finder];
            slow = nums[slow];
            System.out.println("finder=" + finder + ",slow=" + slow);
            if (finder == slow)
                break;
        }
        return slow;
    }
}

2. 环形链表II

解法3的链表形式。

class Solution {
    static class ListNode {
        int val;
        ListNode next;

        ListNode(int x) {
            val = x;
            next = null;
        }
    }

    // 给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
    public static ListNode detectCycle(ListNode head) {
        ListNode slow = head, fast = head;
        while (true) {
            if (fast == null || fast.next == null)
                return null;
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast)
                break;
        }

        while (true) {
            if (head == slow)
                break;
            // System.out.println(head.val);
            head = head.next;
            slow = slow.next;

        }
        return slow;
    }

    public static void main(String[] args) {

        ListNode head = new ListNode(3);
        ListNode second = new ListNode(2);
        ListNode third = new ListNode(0);
        ListNode fourth = new ListNode(-4);
        head.next = second;
        second.next = third;
        third.next = fourth;
        // fourth.next = second;
        System.out.println(detectCycle(head).val);
    }
}

3. 关于为何会在环的入口相遇的证明：

程序中，fast每次循环移动两次，slow每次移动一次，也就是说fast的速度是slow的2倍。

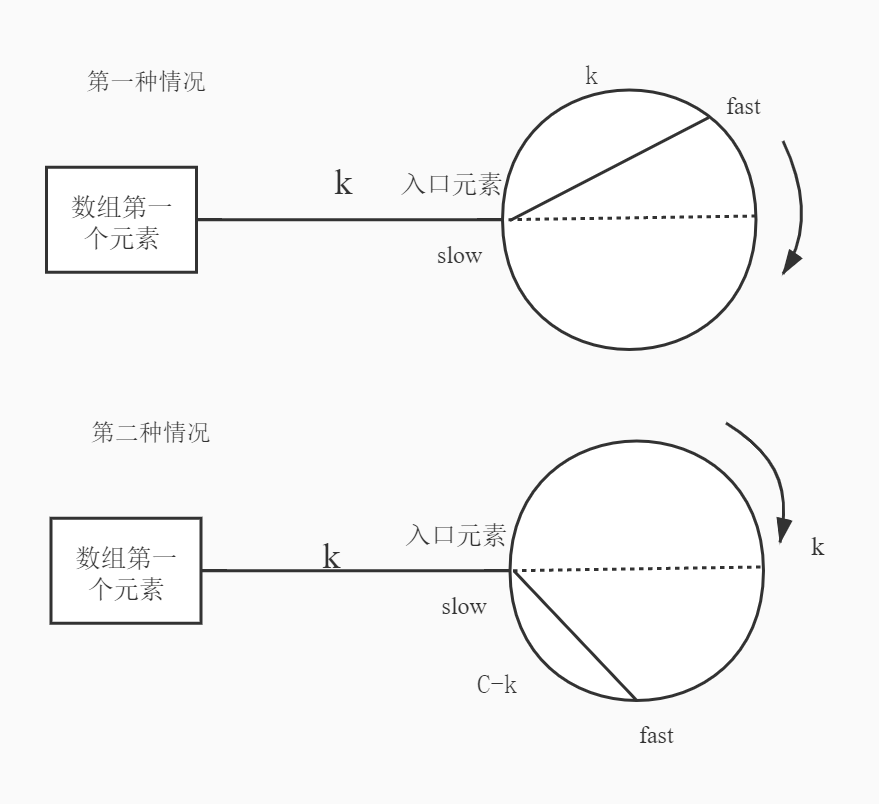
我们假设从索引为$0$元素开始，到环入口元素的距离为$k$，我们把入口元素作为环的起点。

当slow指针刚到达入口元素时，经过了 $k$ 次移动，即：从数组第一个元素到环入口元素有 $k$ 个距离，而此时，fast指针已经在环上了，且领先slow指针 $k$ 个距离，接下来就要分情况讨论了，假设环的周长为 $C$:

当 $k < \frac{C}{2}$ 时,也就是说fast当前位置在环的上半部分，fast在slow的前面（顺时针移动）。

如果此时slow与fast相遇，fast一定会比slow多跑一圈，假设经过了 $t_1$ 时间，fast跑完一圈又回到了slow刚进入圆环时，fast的位置，由于fast的速度是slow的2倍，且slow从0点出发，fast跑完一圈，slow刚好在半圆位置。此时，二者距离为$\frac{C}{2} - k$，假设再经过 $t_2$ 时间，fast与slow相遇，考虑一下：

slow经过的距离：$t_2$ (slow每次移动一格)

fast经过的距离：$2t_2$

可知有如下关系：
$t_2 + \frac{C}{2}-k = 2t_2$ $t_2 = \frac{C}{2} - k$
此时，slow指针的位置为：
$\frac{C}{2} + \frac{C}{2} - k$
与起点距离为：
$C - C + k = k$
而数组第一个元素与圆环入口元素距离也为$k$。

因此，另一个指针从数组第一个元素开始，slow从与fast相遇位置开始一起每次移动一格，最终会在入口元素相遇。
当$k > \frac{C}{2}$时，fast当前位置在环的下半部分。fast在slow后面，距离为$C - k$

这种情况，fast指针不必多跑一圈才能追上slow指针，假设经过$t_3$时间，fast追上了slow。

期间：

fast移动的距离：$2t_3$

slow移动的距离：$t_3$

有如下关系：
$2t_3 = t_3 + C - k$ $t_3 = C - k$
此时slow的位置在$C-k$初，距离达圆环入口处（顺时针移动），有
$C - (C-k) = k$
同样是k个距离。

得证。