摄像机模型与标定

2021-01-02

摄像机模型与标定

参考：计算机视觉，鲁鹏，北京邮电大学。https://www.bilibili.com/video/BV1nz4y197Qv

课件：https://gitee.com/cv-xueba/A01_cvclass_basic

1 摄像机模型

1.1 针孔模型

Q: 如果直接将胶片放置在物体前面，能否成像？不可以，胶片上的某个点汇集了现实世界中各个点的光线，形成的像是模糊的。

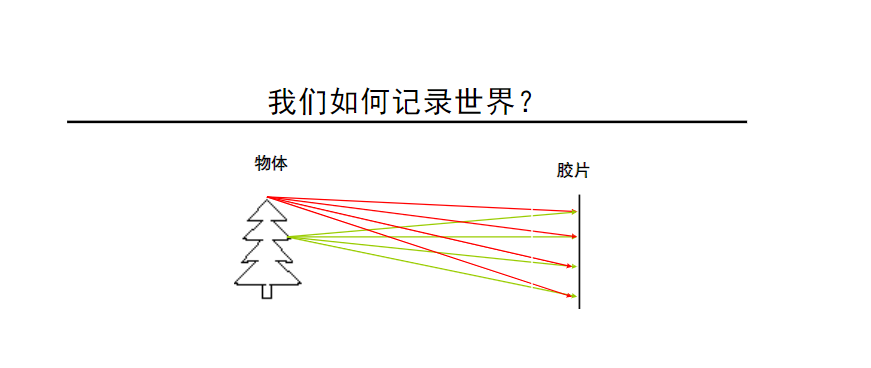
现实中我们发现了小孔成像原理，实现了三维世界到二维的映射。

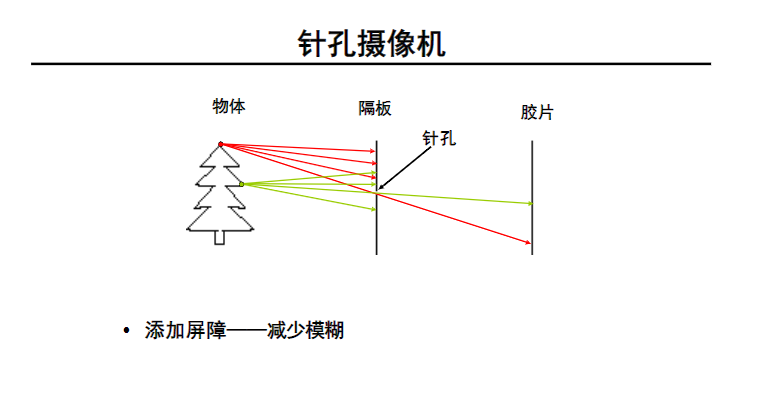
在摄像机中，光圈充当了小孔的作用。

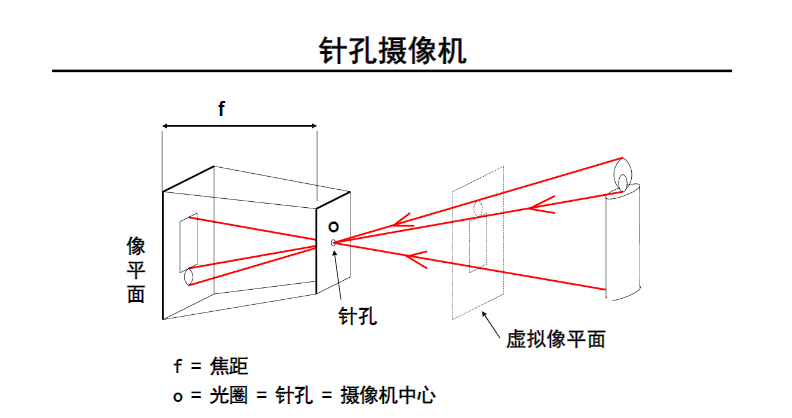
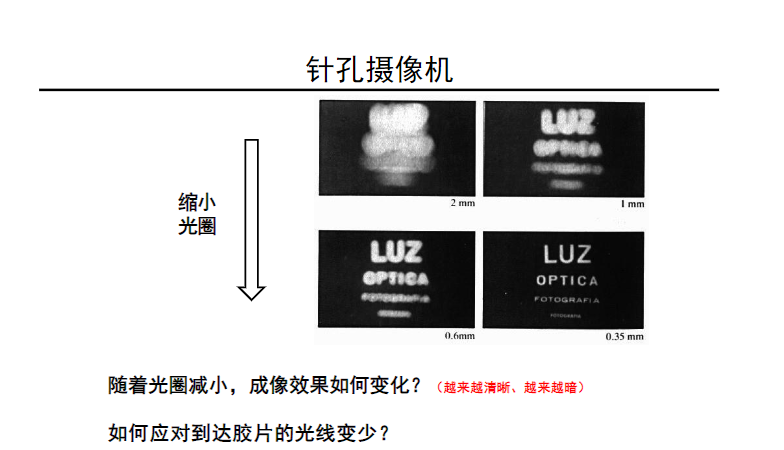
光圈的作用？：光圈越大，进光量越大，成像亮度越大，但是模糊；光圈越小，成像亮度越小，但是清晰。如何折衷？加透镜，聚光！

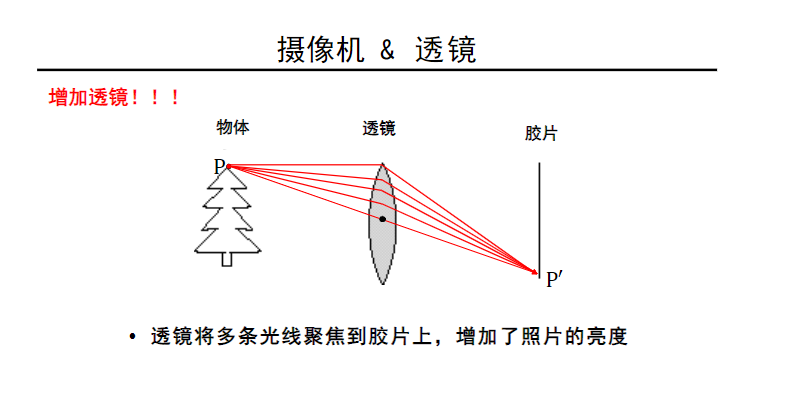
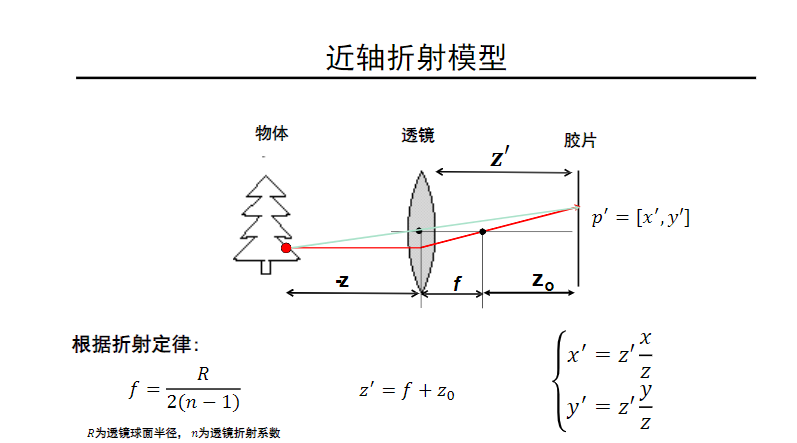
透镜将多条光线聚焦到胶片上，增加了照片的亮度；所有平行于光轴的光线都会会聚到焦点，焦点到透镜中心的距离称为焦距；穿过透镜中心（光心）的光线的传播方向不发生改变。

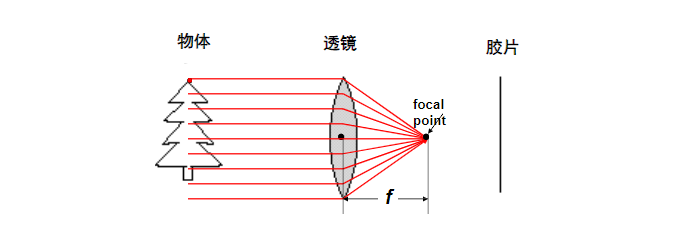
透镜存在问题：当像距（景深）不合适的话会失焦、径向畸变。

1.2 摄像机几何

本节要介绍的坐标系：摄像机坐标系、像平面坐标系、像素坐标系、世界坐标系，齐次坐标。

1.2.1 摄像机坐标系和像平面之间的坐标变换关系

图10

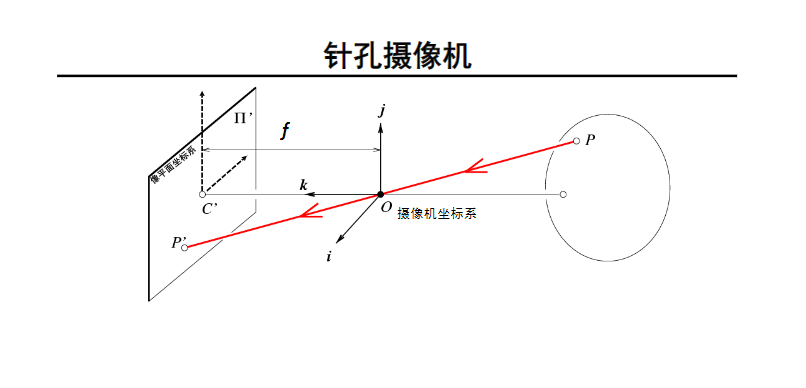
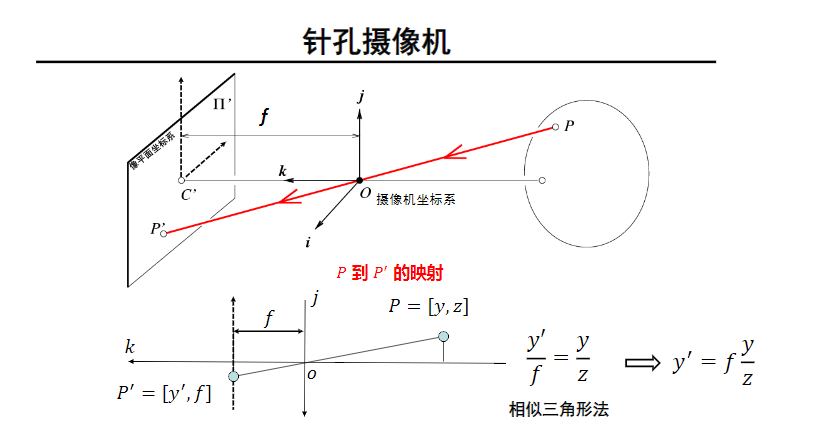
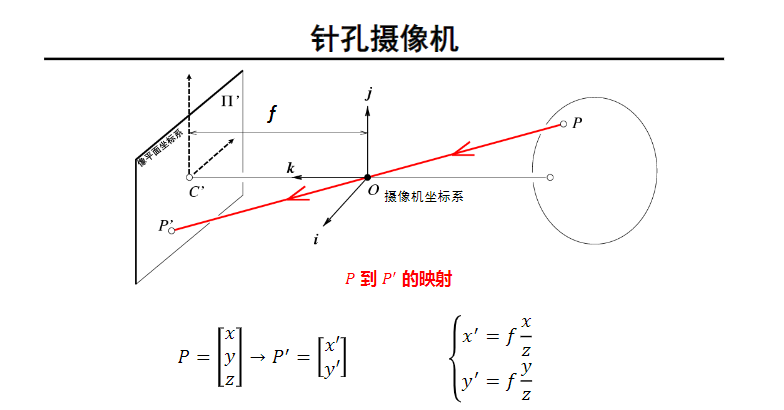
加了透镜之后的相机模型：

图11

1.2.2 像平面坐标系和像素坐标系之间的变换关系

图12

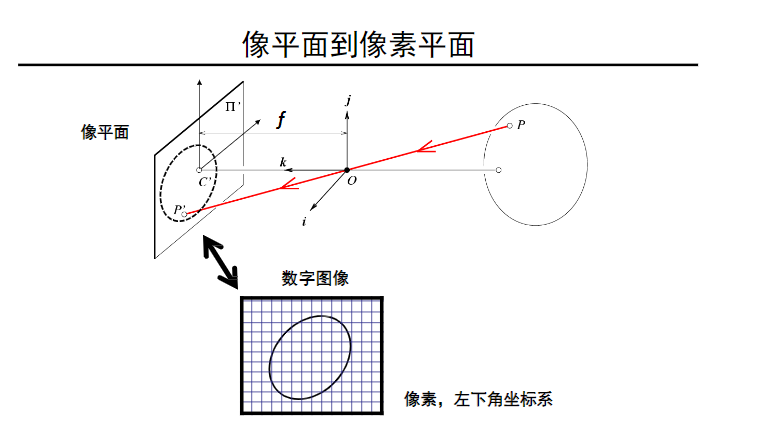
在像平面坐标系中，原点是在中心点（$C^\prime $）；而在像素平面中，一般以左下角为原点。因此，从像平面坐标系到像素平面有$x,y$方向上的两个偏置$c_x,c_y$。

图13

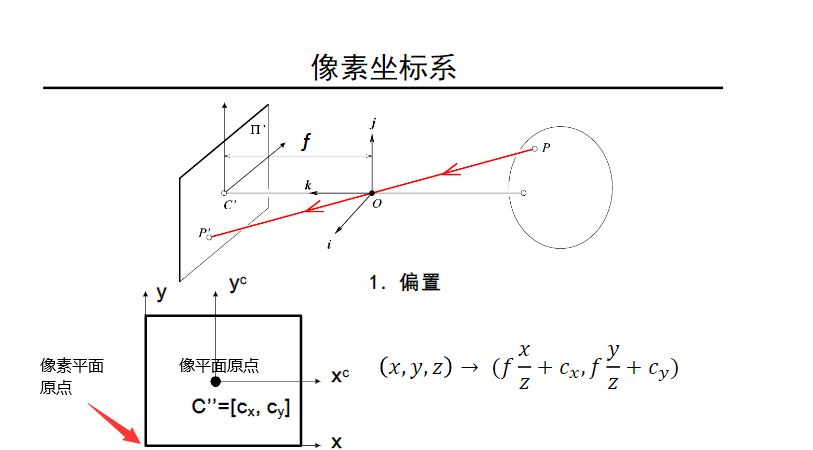
上图中我们可以看出，在摄像机坐标系平面中的点$(x,y,z)$在像平面中的坐标是$(f\frac{x}{z},f\frac{y}{z})$，在像素平面中，像平面原点坐标是$(c_x,c_y)$，因此摄像机坐标系的点到像素坐标系坐标变换为：$(f\frac{x}{z} + c_x,f\frac{y}{z}+c_y)$。

但还有一个问题是，$x,y$都是现实世界中的点，单位都是米/厘米等（$m/cm$）我们想转换为像素单位（$pixel$）。这就涉及到相机成像元器件（CCD/CMOS等）的分辨率 $k,l$ （垂直方向、水平方向各向异性）决定了一个像素可以代表现实世界中多少距离。

因此，有单位变换：

$(x,y,z) \Rightarrow (fk\frac{x}{z},fl\frac{y}{z})$

$f$ 的单位是$m$，那么$k,l$ 的单位是$pixel/m$，令$\alpha = fk,\beta = fl$，有：

$P=(x,y,z) \rightarrow P^\prime=(\alpha\frac{x}{z},\beta\frac{y}{z})$

$P^\prime$ 的单位就是像素了，表示像素平面坐标中的点。

注意：这个变换不是线性的（$z$ 是变换的）。

1.2.3 摄像机坐标系和像素平面坐标系之间的关系

我们想把这个变换表示为线性形式，这时就需要引入齐次坐标。齐次坐标就是将一个原本是 $n$ 维的向量用一个 $n+1$ 维向量来表示。二维笛卡尔坐标系的点 $(x,y)$ 变换到齐次坐标就是 $(x,y,1)$；而齐次坐标系中的点 $(x,y,z)$变换到二维笛卡尔坐标中就是 $(x/z,y/z)$，$(x,y,z,w)\rightarrow (x/w,y/w,z/w)$。

齐次坐标系中的投影变换

引入齐次坐标后，把$P=(x,y,z)$表示为齐次坐标，即$P_h=(x,y,z,1)$，通过下面变换

$P_h^\prime = \begin{pmatrix}\alpha x + c_xz\\\beta x + c_yz\\z\end{pmatrix}=\begin{pmatrix}\alpha&0&c_X&0\\0&\beta&c_y&0\\0&0&1&0\end{pmatrix}\begin{pmatrix}x\\y\\z\\1\end{pmatrix}$

欧式点$(\alpha\frac{x}{z},\beta\frac{y}{z})$变换到齐次坐标对应$\begin{pmatrix}\alpha x + c_xz\\\beta x + c_yz\\z\end{pmatrix}$（同除 $z$ 就变回去了），有了上式中的投影矩阵，可以直接进行变换并且是线性的。

$M =\begin{pmatrix}\alpha&0&c_X&0\\0&\beta&c_y&0\\0&0&1&0\end{pmatrix}$

称 $M$ 即投影矩阵。考虑倾角$\theta$，

图14

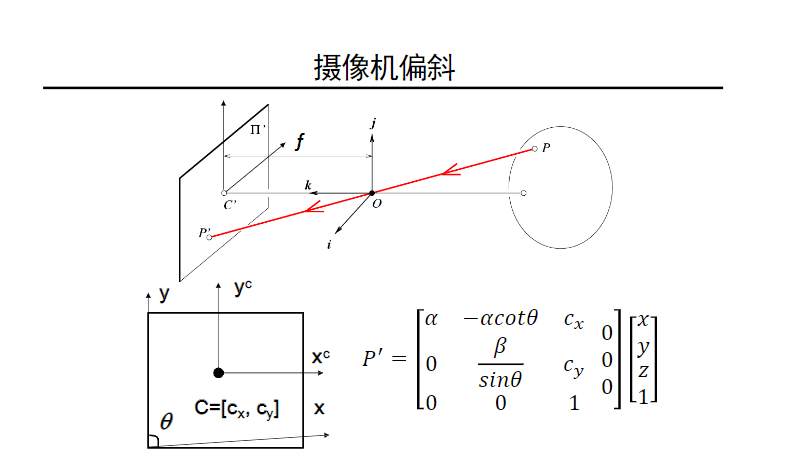
$M$ 就变成了：

$M =\begin{pmatrix}\alpha&-\alpha\cot\theta &c_x&0\\0&\frac{\beta}{\sin \theta}&c_y&0\\0&0&1&0\end{pmatrix}$

这就是摄像机世界和像素平面的映射关系。

$K =\begin{pmatrix}\alpha&-\alpha\cot\theta &c_x\\0&\frac{\beta}{\sin \theta}&c_y\\0&0&1\end{pmatrix}$

K为被称为摄像机内参数矩阵，内参数决定了摄像机坐标系下空间点到图像点的映射。

$M = K[I\ O]$

注意：上面是在齐次坐标下的表示。

1.2.4 世界坐标系与摄像机坐标系之间的关系

齐次坐标表示：

$P = RPw + T = \begin{pmatrix}R&T\\O&1\end{pmatrix}P_w$

$R_{3\times3}$表示三维空间的旋转矩阵，$T_{3\times1}$表示三维空间平移向量。$P_w=(x_w,y_w,z_w,1)$表示世界坐标系下的点，$P$表示摄像机坐标系下的点。

1.2.5 世界坐标系与像素平面坐标系变换

$P^\prime =K(I\ O)P = K(I\ O) \begin{pmatrix}R&T\\O&1 \end{pmatrix}P_w =K(R\ T)P_w$

上面就是世界坐标系下的点到像素平面坐标系的变换，最后的$P^\prime_{3\times1}$是像素点的齐次坐标向量。与摄像机内参矩阵相对应，我们称$\begin{pmatrix}R&T\\0&1 \end{pmatrix}$为外参数矩阵。

图15

Q：投影矩阵$M$有多少个自由度（参数）？ A：$R$ 有三个自由度，$T$ 有三个自由度，$K$ 有五个自由度，因此$M$ 有十一个自由度。

图16

2 摄像机的标定

任务：给定图像数据集，求解摄像机的内参数。

重要性：摄像机内、外参数描述了三维世界到二素的映射关系。

图17

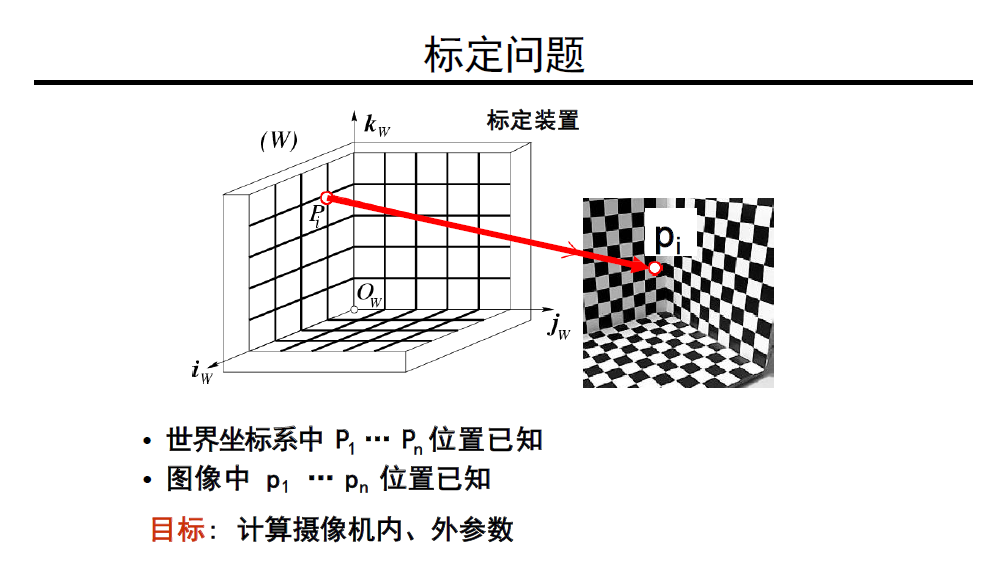
像素平面的点非齐次坐标$p = \begin{pmatrix}u\\v\end{pmatrix}$，世界坐标系中的点齐次坐标$P=\begin{pmatrix}x\\y\\z\\1\end{pmatrix}$，投影矩阵$M=\begin{pmatrix}\pmb m_1\\\pmb m_2\\\pmb m_3\end{pmatrix}$，可知 $\pmb m$ 是$1\times 4$的行向量。因此有：

$p^\prime =MP=\begin{pmatrix}\pmb m_1\\\pmb m_2\\\pmb m_3\end{pmatrix}P=\begin{pmatrix}\pmb m_1P\\\pmb m_2P\\\pmb m_3P\end{pmatrix}$

注意$p^\prime$是齐次坐标形式，因此有：

$\begin{pmatrix}u\\v\end{pmatrix} = \begin{pmatrix}\frac{\pmb m_1P}{\pmb m_3P}&\frac{\pmb m_2P}{\pmb m_3P}\end{pmatrix}^T$

在实际标定中，每一个点的$u,v,P$我们都是可以知道的，那么求解的未知量就只剩下了$\pmb m_1,\pmb m_2,\pmb m_3$这三个向量（共包含11个未知量）。

图18