数据结构之堆

2021-01-02

数据结构之堆

堆就是用数组实现的二叉树，所以它没有使用父指针或者子指针。

堆的定义（性质）：

堆中某个节点的值总是不大于或不小于其父节点的值；
堆是一棵完全二叉树

根元素为最大值的称为大根堆，根元素为最小值的称为小根堆。

在堆中：

数组索引为i的元素其父元素索引是：floor((i - 1) / 2)``floor即取下界（floor(3.5)=3）；
数组索引为i的元素，左孩子节点的索引是：2i + 1，右孩子节点的索引是：2i + 2。

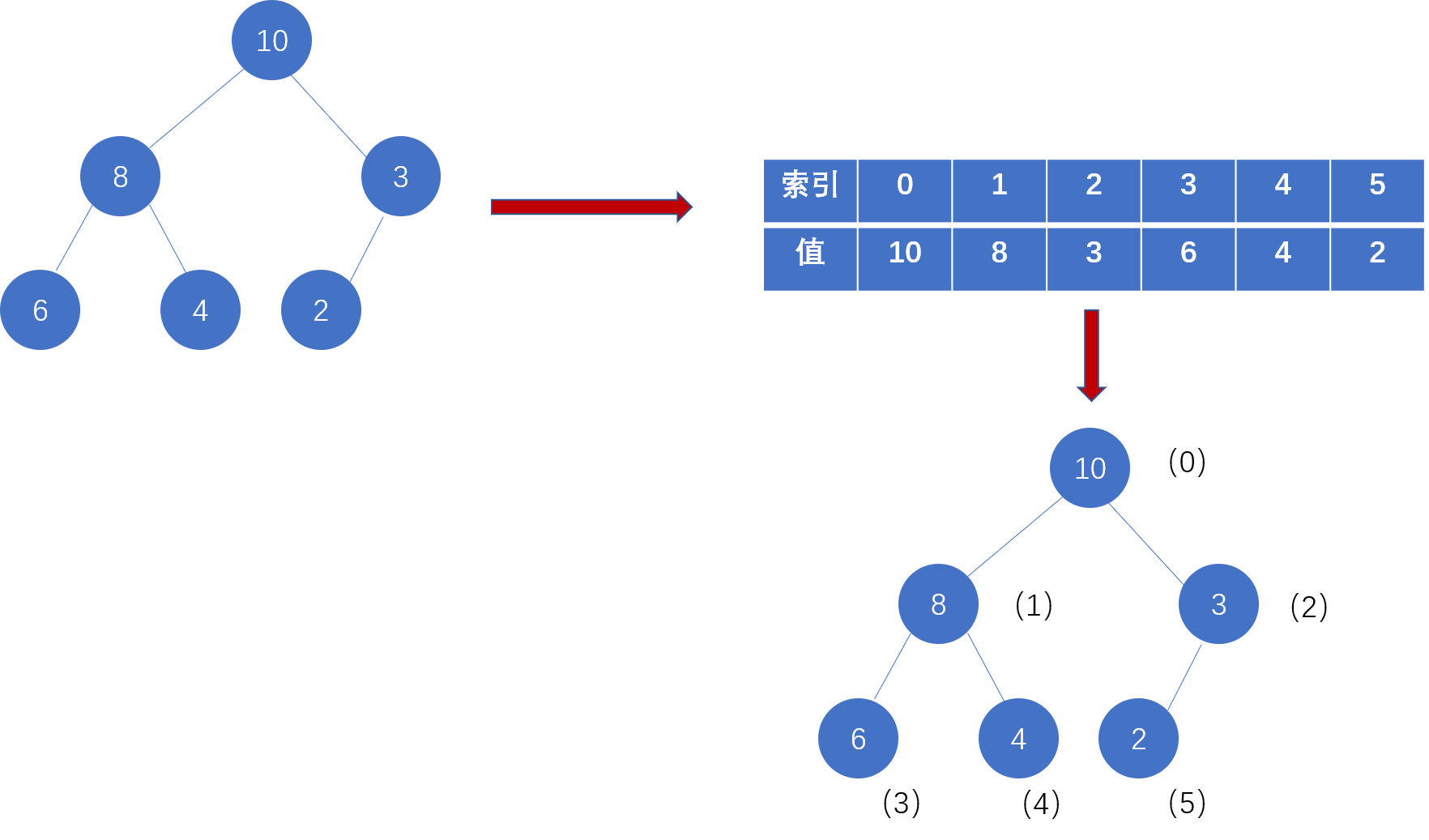
给定如下所示一个大根堆，用数组存储就是[10,8,3,6,4,2]。换句话说，这样的数组可以抽象化成一棵完全二叉树。可以看到没有用到任何指针，数组中索引为i的元素通过上述公式来找到对应的父节点和孩子节点。

现在的问题就是：给定一个无序数组，如何构建一个堆？构建好以后，添加元素、删除元素该怎么调整堆？

关于维护堆两个重要的操作就是heapifyUp和heapifyDown。

以小根堆为例。

添加元素：heapifyUp，若当前节点值小于父节点，那么就交换，直到到达根节点为止（不断冒泡）。添加元素时，由于是数组，我们一般直接添加到数组最后，然后对新添加的元素不断执行heapifyUp进行维护。向上调整的时间复杂度是 $O(\log n)$ 的。

删除元素：heapifyDown。删除根节点时，令其和数组最后一个元素进行交换，这样删除最后一个元素的时间复杂度仅为 $O(1)$。然后我们对新的根节点执行heapifyDown操作即可。

构建堆：从最后一个非叶子节点开始，依次执行heapfiyDown操作。

class Heap{
	private int[] data;
    
    public Heap(int[] nums){
        this.data = nums;
        //传入一个数组构建成 大根堆
        int n = data.length;
        // 从最后一个元素的父节点开始即 (n-1)/2 
        for (int i = (n-1)/2; i >= 0; i--){
            heapifyDown(i,n-1);
        }
        // 或者
        //for (int i = 0; i <  n; i++){
            //heapifyUp(i);
        //}
    }

    public void heapifyDown(int index, int end){
        int j = 2 * index + 1;
        if (j > end){
            return ;
        }
        // 如果右子树存在且大于左子树
        if (j + 1 <= end && data[j+1] > data[j]){
            j++;
        }
        if (data[index] >= data[j]){
            return;
        }
        swap(j, index);
        heapifyDown(j, end);
    }
    
    public void heapifyUp(int index){
        int parent = (index-1) / 2;
        if (parent < 0){
            return;
        }
        if (data[parent] >= data[index]){
            return;
        }
        swap(index, parent);
        heapifyUp(parent);
    }
    
    private void swap(int a, int b){
    	int tmp = data[a];
        data[a] = data[b];
        data[b] = tmp;
    }
    
    public void sort(){
        int len = data.length ;
        for (int i = len - 1; i >= 1; ){
            swap(i,0);
            i--;
            heapifyDown(0,i);
        }
    }
}

堆排序和优先队列

将一个数组构建成堆，然后不断的删除堆的根节点，根节点的值依照删除顺序就会形成一个有序数组，这就是堆排序。堆排序的时间性能$O(n\log n)$。优先队列本质上还是一个先进先出的队列，每次出队的元素都是满足定义的优先规则的元素。