朴素贝叶斯（Naive Bayes）

2021-01-02

朴素贝叶斯（Naive Bayes）

1. 条件概率和全概率公式（由因到果）

首先给出条件概率公式：

$P(A|B) = \frac{P(AB)}{P(B)}$

$P(AB)$是变量$A$和$B$的联合概率分布，$P(B)$是变量 B 的边缘概率分布。

全概率公式：

若事件$Y_1，Y_2，…$构成一个完备事件组且都有正概率，则对任意一个事件$X$，有如下公式成立：

$P(X) = \sum_{i}P(X|Y_i)P(Y_i)$

解释：全概率公式的意义在于，当某一事件的概率难以求得时，可转化为在一系列条件下发生概率的和。

乘法定理：

$P(A_1,A_2,A_3,...,A_n) = P(A_1)P(A_2|A_1)P(A_3|A_1,A_2)···P(A_n|A_1,A_2,...A_{n-1})$

2. 贝叶斯公式（执果索因）

贝叶斯公式就是当已知结果，问导致这个结果的第i原因的概率是多少。(转化到分类问题上，“结果”就是样本，“第i个原因”即属于哪个类别)。

由条件概率公式，可以写成：

$P(Y_i|X) = \frac{P(XY_i)}{P(X)} = \frac{P(X|Y_i)P(Y_i)}{P(X)}$

结合全概率公式，有:

$P(Y_i|X) = \frac{P(X|Y_i)P(Y_i)}{\sum_{j}P(X|Y_j)P(Y_j)}$

解释：我们把$P(Y_i)$叫做$Y$的先验概率，$P(Y_i|X)$称为后验概率。

下面介绍一个例子实际计算一下。

3. 朴素贝叶斯

朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。朴素贝叶斯算法假设了给定样本情况下，数据集属性之间是相互条件独立这一朴素假设 ，因此算法的逻辑性十分简单，并且算法较为稳定，当数据呈现不同的特点时，朴素贝叶斯的分类性能不会有太大的差异。换句话说就是朴素贝叶斯算法的健壮性比较好，对于不同类型的数据集不会呈现出太大的差异性。当数据集属性之间的关系相对比较独立时，朴素贝叶斯分类算法会有较好的效果。

下面给出朴素贝叶斯的推导和数学定义。

设有样本数据集$D=\{d_1,d_2,···,d_n\}$，每个样本特征属性集$X=\{x_1,x_2,···，x_d\}$，这$n$个样本共存在$m$个分类 $Y=\{y_1,y_2,···,y_m\}$，其中$x_1,x_2,···,x_d$x 相互独立且随机。则先验概率$P(Y)$，后验概率$P(Y|X)$.

由于各个特征之间相互独立，在给定类别 $y$ 情况下，$P(X|Y)$进一步可以表示为：

$P(X|Y =y_j) = \prod_{i = 1}^{d} P(x_i|Y = y_j)$

实际上是乘法定理和条件独立的应用。

结合贝叶斯公式，有：

$P(y_i|x_1,x_2,···,x_d) = \frac{P(y_i)\prod_{j = 1}^{d}P(x_j|y_i)}{\sum_k^{m}P(y_k)\prod_j^{d}P(x_j|y_k)}$

在给定样本的情况下，计算样本属于各个类别的概率时，分母都相等。

从而，只需最大化分子。有：

$P(y_i|x_1,x_2,···,x_d) ∝ P(y_i)\prod_{j = 1}^{d}P(x_j|y_i)$

从而

$\hat{y} = arg \max_{y_i}P(y_i)\prod_{j = 1}^{d}P(x_j|y_i),y_i \in Y$

，这就是朴素贝叶斯定理。可能结果需要归一化，即各个类别概率加起来和为$1$。

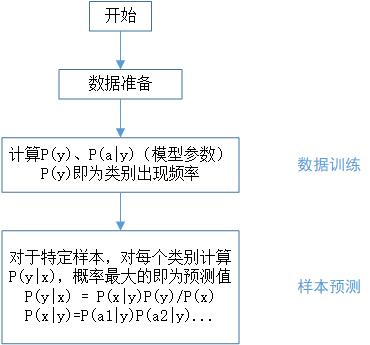
给定样本$X$，类别为 $y_i$ 的概率（m为类别个数）即：

$P(y_i|x_1,x_2,...,x_d) = \frac{P(y_i)\prod_{j = 1}^{d}P(x_j|y_i)}{\sum_{i = 1}^{m}[P(y_i)\prod_{j = 1}^{d}P(x_j|y_i)]}$

最大的概率即为预测类别。这就是朴素贝叶斯。

“朴素在哪里？”

事实上，朴素贝叶斯做了如下假设：

一个特征出现的概率，与其他特征独立
每个特征同等重要

在真实的数据中，这个假设有可能并不会成立，如果一本书中出现了“机器学习”这个词，那么有很大概率会出现“数据挖掘”“特征工程”等词语，而出现“少林功夫”的概率是很低的。由此看来，词之间的概率并不独立，而且词对于分类的概率影响很大，每个词的重要性也是不同的。

因此，这样做出的假设是很“天真”，很”朴素“的。

4. 垃圾邮件识别

现在有已经分好类别的垃圾邮件和非垃圾邮件，希望训练一个垃圾邮件过滤器。有一个想法是分别统计垃圾邮件和非垃圾邮件中所包含的单词，在测试时，只要分析给定邮件中的单词，来计算这封邮件是垃圾邮件还是正常的邮件（其他算法分析单词顺序更加有效，这里不做介绍）。下面给出更加形象化定义。

“朴素”：因为一封邮件中可能既包含$W_1$、又包含$W_2$，朴素就是假设$W_1$、$W_2$…相互独立。

同理可以计算

$P(ham|W_1,W_2,...) ∝ P(W_1|ham)P(W_2|ham)...P(ham)$

最后将二者概率进行归一化，就可得出是垃圾邮件还是正常邮件的概率。

$P(ham|W_1,W_2,...) = \frac{P(W_1|ham)P(W_2|ham)...P(ham)}{P(W_1|ham)P(W_2|ham)...P(ham)+P(W_1|spam)P(W_2|spam)...P(spam)}$

5 生成模型和判别模型

判别模型(discriminative model)

通过求解条件概率分布 $P(y|x)$ 或者直接计算 $y$ 的值来预测 $y$。如：线性回归（Linear Regression）,逻辑回归（Logistic Regression）,支持向量机（SVM）, 传统神经网络（Traditional Neural Networks）,线性判别分析（Linear Discriminative Analysis），条件随机场（Conditional Random Field）。
生成模型(generative model)

通过对观测值和标注数据计算联合概率分布 $P(x,y)$ ，再计算$P(y|x)$来达到判定估算 $y$ 的目的。朴素贝叶斯（Naive Bayes）, 隐马尔科夫模型（HMM）,贝叶斯网络（Bayesian Networks）和隐含狄利克雷分布（Latent Dirichlet Allocation）、混合高斯模型（GMM）。

6 贝叶斯网络

贝叶斯网络(Bayesian network)，又称信念网络(Belief Network)，或有向无环图模型(directed acyclic graphical model)，是一种概率图模型，于 1985 年由 Judea Pearl 首先提出。它是一种模拟人类推理过程中因果关系的不确定性处理模型，其网络拓朴结构是一个有向无环图(DAG)。

贝叶斯网络的有向无环图中的节点表示随机变量{X1,X2,...,Xn}{X1,X2,...,Xn}。它们可以是可观察到的变量，或隐变量、未知参数等。认为有因果关系（或非条件独立）的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(children)”，两节点就会产生一个条件概率值。一个简单的贝叶斯网络如下图：

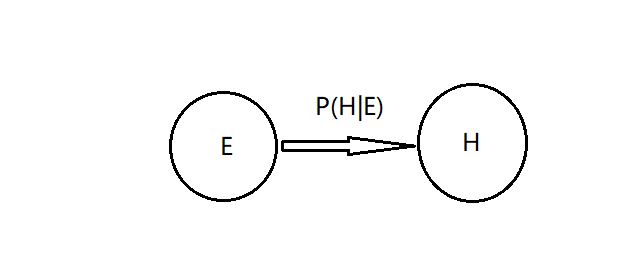
例如，假设节点 E 直接影响到节点 H，即$E→H$，则用从$E$指向$H$的箭头建立结点$E$到结点$H$的有向弧(E,H)，权值(即连接强度)用条件概率$P(H|E)$来表示，如下图所示：

贝叶斯网络中，全部随机变量的联合分布如下：

$P(x_1,x_2,···,x_n) = \prod_{i = 1}^{n} P(x_i|parent(x_i))$

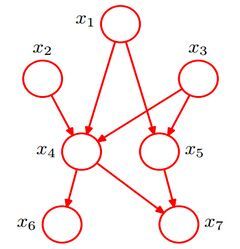
比如上图的贝叶斯网络中，$x_1,x_2,x_3,…,x_7$的联合概率分布是：

$P(x_1,x_2,...,x_7) = p(x_1)p(x_2)p(x_3)p(x_4|x_1,x_2,x_3)p(x_5|x_1,x_3)p(x_6|x_4)p(x_7|x_4,x_5)$

下面介绍贝叶斯网络的结构形式：

head-to-head

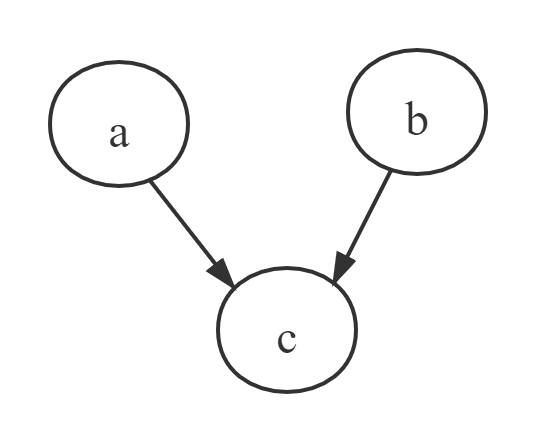
在 $c$ 未知的情况下，$a$ ，$b$ 被阻断（blocked），是独立的。
tail-to-tail

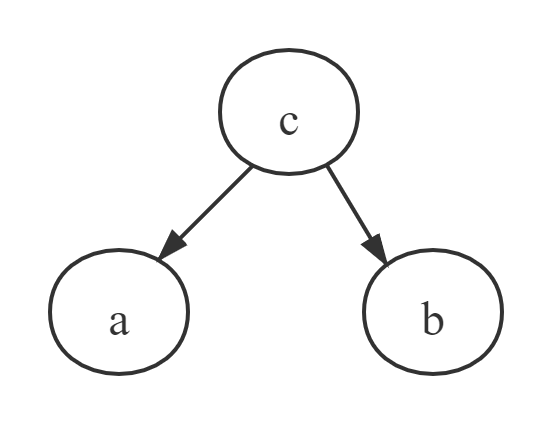
在 $c$ 给定的情况下，$a$ ，$b$ 是独立的。
head-to-tail

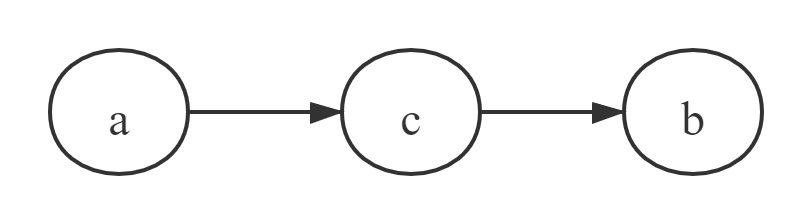
在 $c$ 给定的情况下，$a$ ，$b$ 被阻断（blocked），是独立的。其实这就是马尔可夫链，当前状态只与前一个状态相关。