机器视觉基础Lecture 3局部特征

Lecture 3 局部特征

1. Harris角点检测

1.1 特征点需要满足的性质

可重复性/区分性/容易计算

为什么选角点？

一个窗口在图像上滑动，处于平坦（flat）区域时，窗口内的内容不会发生明显改变；处于边缘（edge）区域时，只有沿一个方向（竖直或水平）滑动会发生变化；而处于角点（corner）区域时，沿两个方向滑动窗口内容都会发生改变。

1.2 角点

$$E(u,v) = \sum_{x,y} w(x,y)[I(x + u, y + v) - I(x,y)]^2$$

说明：$x,y$的取值范围是窗口的范围；$w(x,y)$指权值函数，比如$Gaussian$函数，本质上取到一个加权的作用。$u,v$即平移的距离。$E(u,v)$表示窗口内容变化程度。

我们希望直接观察到$u,v$和$E(u,v)$之间的关系，而上式定义较麻烦不直观（还得通过$I(x,y)$），怎么直接建立关系呢？答案：二维泰勒展开！

$$E(u,v) \approx E(0,0) + [u,v]\begin{pmatrix}E_u(0,0)\\E_v(0,0)\end{pmatrix} +\frac{1}{2}[u,v]\begin{pmatrix}E_{uu}&E_{uv}\\E_{vu}&E_{vv}\end{pmatrix}\left [\begin{matrix}u\\v\end{matrix} \right]$$ $$E(0,0) = 0$$ $$E_{u}(u,v) = \sum_{x,y}2w(x,y)[I(x+u,y+v)-I(x,y)]I_x(x+u,y+v)$$

将(0,0)带入：得：$E_u(0,0) = 0$；同理可得$E_v(0,0)=0$；

为了表示方便，令：$I(x+u,y+v)$简写为$I$，$I_x(x+u,y+v)$简写为$I_x$等

$$E_{uu}(u,v) = \sum_{x,y}2w(x,y)I_xI_x+\sum_{x,y}2w(x,y)[I-I(x,y)]I_{xx}$$ $$E_{uv}(u,v) =\sum_{x,y}2w(x,y)I_yI_x+\sum_{x,y}2w(x,y)[I-I(x,y)]I_{xy}$$

带(0,0)有：

$$E_{uu}(0,0) = \sum_{x,y}2w(x,y)I_x(x,y)I_x(x,y)\\ E_{vv}(0,0) = \sum_{x,y}2w(x,y)I_y(x,y)I_y(x,y)\\ E_{uv}(0,0) =E_{vu}(0,0)= \sum_{x,y}2w(x,y)I_x(x,y)I_y(x,y)$$

即：

$$E(u,v) \approx [u,v]M\left[ \begin{matrix}u\\v\end{matrix} \right]$$ $$M_{2\times2} = \sum_{x,y}w(x,y)\left[\begin{matrix}I_x^2&I_xI_y\\I_xI_y&I_y^2\end{matrix}\right] = \left[\begin{matrix}\lambda_1&0\\0&\lambda_2\end{matrix}\right]$$

$I_x,I_y$即上一个Lecture讲过的图像上定义的梯度（同方向相邻两个像素的差值）。$M$被称为second moment matrix。它是一个对称正定矩阵，因此可以对角化为特征值组成的对角矩阵。

考虑：

$$E(u,v) = \lambda_1u^2 + \lambda_2v^2=C,C\in R$$

可知$E(u,v)$在几何上是一个椭圆。其轴分别为$1/\sqrt\lambda_1,1/\sqrt\lambda_2$。

$\lambda_1,\lambda_2$表示窗口内的$x,y$方向的图像梯度。当两个方向变化都很大时可能为角点。

$$R = \det(M) - \alpha *trace(M)^2 = \lambda_1\lambda_2-\alpha(\lambda_1+\lambda_2)^2$$

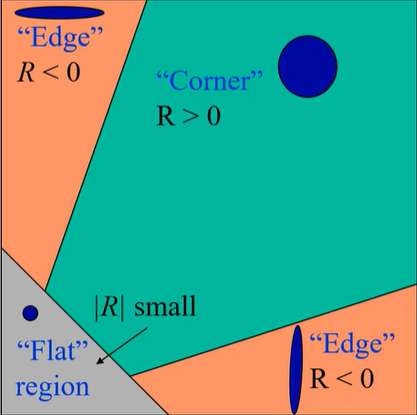
优点：对光照、亮度不敏感

缺点：对尺度（scale）变换敏感！

2. Blob Detection

3. SIFT

SIFT即尺度不变特征变换。光照、尺度、旋转、平移。

添加仿射自适应：更好的处理视角

观察dog图像和log图像发现他俩走势几乎一致，可以用dog来代替log提高计算效率

sift $4 \times 4 \times 8=128$ 维描述子，sift算法将邻域内像素划分为 $16×16$ 个子域，进一步将其划分为 $4×4$ 块（每个块又是由 $4×4$ 小域组成），具体见下，分别计算每个块内8个方向的梯度方向直方图。所以最终得到 $4×4×8=128$ 4×4×8=128 的描述子向量。

梯度强度直方图：将$[0,2\pi]$划分为8份，也就是说$[0,\frac{\pi}{4}],[\frac{\pi}{4},\frac{\pi}{2}]，…,[\frac{7\pi}{4},2\pi]$。然后在这些小区域（16个像素）的范围内，根据每个像素点的梯度方向所在范围，将该像素点的梯度幅值加到对应的bin上，最后就形成了小区域一个梯度强度直方图（8个数字描述）。16个小区域的整体特征就可以用这个$4 \times 4 \times 8$的特征向量来描述。

在小区域上（16个像素）统计梯度幅值直方图能更好的捕捉局部特征。