极几何与多视图几何
多视图几何的关键问题
- 摄像机几何:从一张或者多张图像中求解摄像机的内、外参数(标定)
- 场景几何:通过二至多张图寻找3D场景坐标
- 对应关系:已知一个图像中 $p$ 点,如何在另外一个图像中找到 $p^\prime$ 点(极几何要解决的问题)。
1. 场景几何引入
已知世界坐标系中一点 $P$ 在两个像素坐标系中对应点分别为 $p,p^\prime$,两个摄像机内外参数均已知,试求出 $P$ 在世界坐标系的坐标。
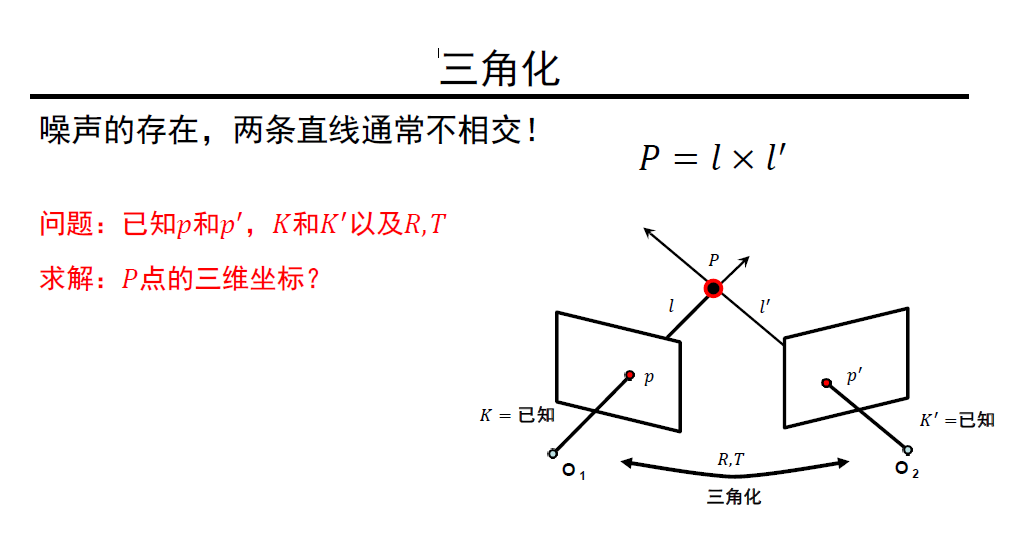
- 线性方法:Multiple view geometry in computer vision
- 非线性解法
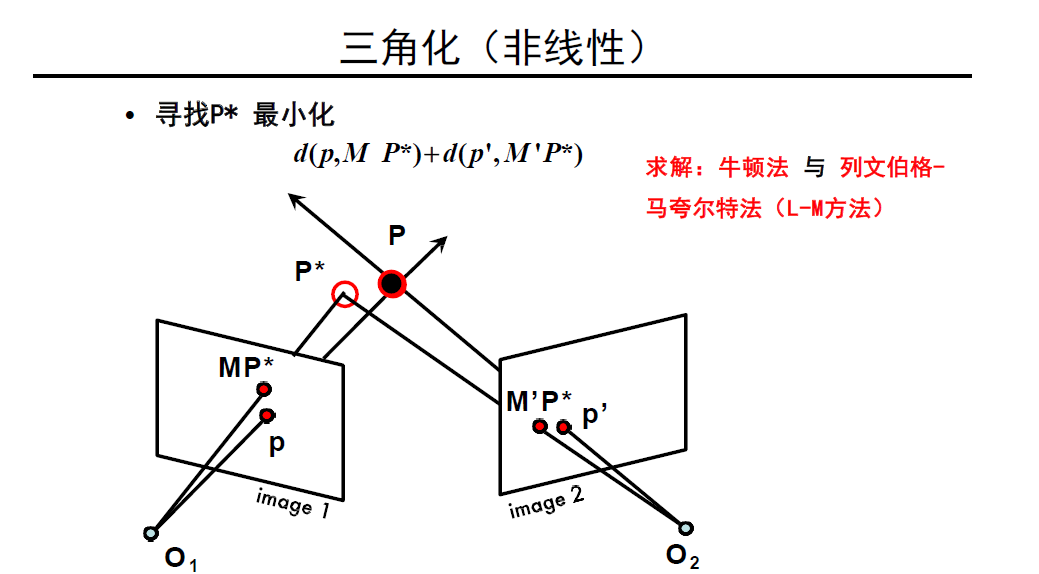
2. 极几何
极几何描述了同一场景或者物体的两个视点图像间的几何关系。
几个重要概念:基线、极点、极平面、极线。
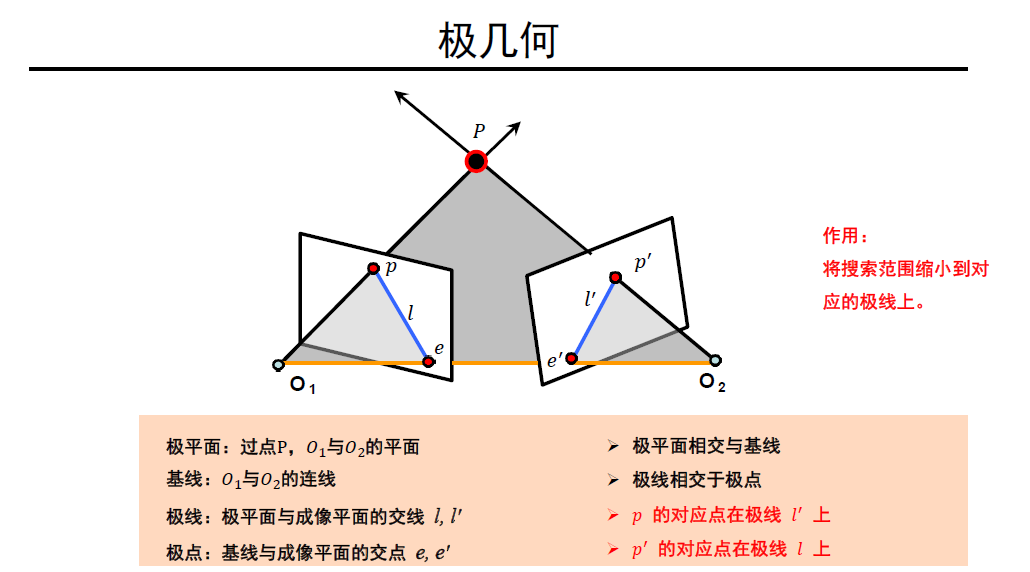
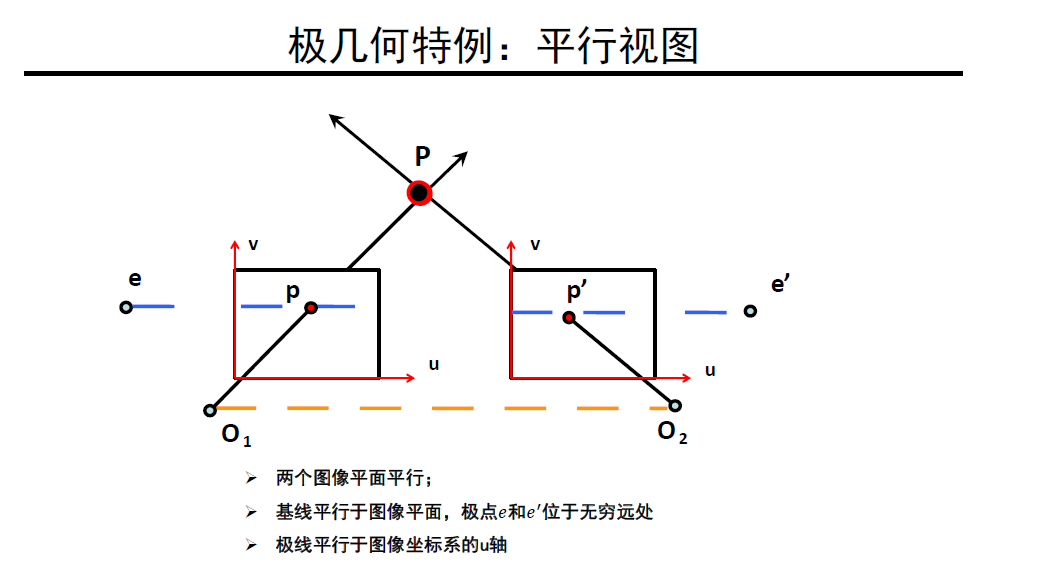
两个特例:
平行视图
前向平移(无旋转)
两幅图上极点的位置相同
2.1 本质矩阵(Essential Matrix)
前置知识:
本质矩阵对规范化摄像机拍的两个视点图间极几何关系进行代数描述。规范化指的就是摄像机内参数矩阵 $K$ 是个三阶单位阵。(复习投影矩阵 $M = K\begin{pmatrix}I&O\end{pmatrix}$,世界坐标系到摄像机坐标系变换:$P=RP_w + \pmb t$)。
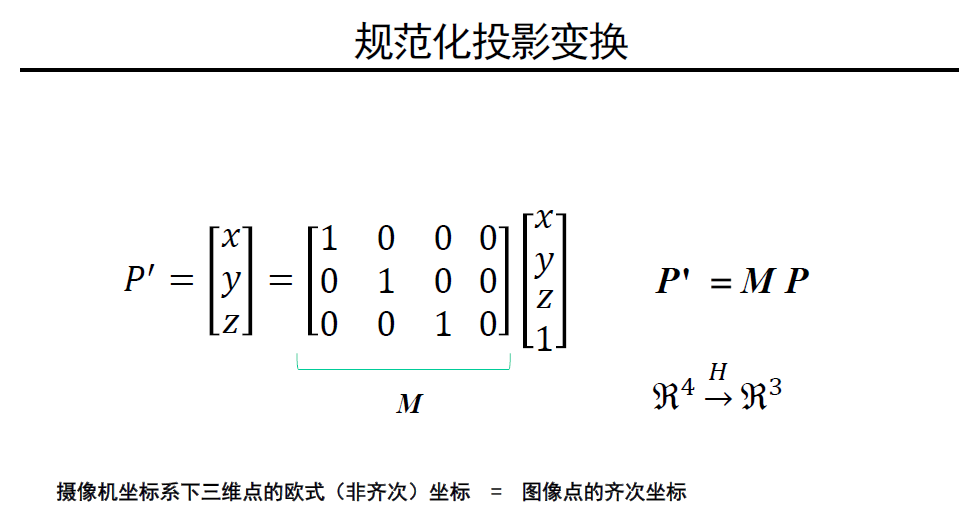
在规范化的条件下,摄像机坐标系下的三维点的欧式坐标和像素点的齐次坐标是相同的。
因此,若图像 $I$ 上点 $p$ 像素坐标为 $(u,v)$,齐次坐标就是 $(u,v,1)$,根据上面讲的对应在摄像机坐标系 $O_1$下的欧式坐标就是 $(u,v,1)$;同理,$p^\prime$ 在 $O_2$坐标系下的欧式坐标是 $(u^\prime,v^\prime,1)$(注意,这儿的1不是固定的,因为齐次坐标下是尺度不变的)。
本质矩阵的作用:
给定 $p$ 在摄像机坐标系 $O_1$下的欧式三维坐标$(u,v,1)$,向量$\pmb p=O_1p = (u,v,1)$,本质矩阵 $E_{3\times3}$,那么极线 $l^\prime$ 的方程($O_1$坐标系下)就是:$E\pmb p=\pmb l^\prime$。对于极线 $l$ 有 $\pmb p^T\pmb l=0$(假设极线 $l$ 的方程为$ax+by+c=0$,那么可以用一个向量表示为$\pmb l=(a,b,c)^T$,又因为 $p$ 点在 $l$ 上,因此$au+bv+c=0$,即 $\pmb p^T\pmb l=0$)。同理,对于 $p^\prime$在$O_2$ 坐标系下的欧式三维坐标$(u^\prime,v^\prime,1)$,$\pmb p^\prime = O_2p^\prime$,有 $\pmb p^{\prime T} \pmb l^\prime = 0$成立,
将$E\pmb p=\pmb l^\prime$带入可得:

叉乘的矩阵表示形式:

本质矩阵的推导:

$\pmb p^\prime = R(\pmb p-\pmb t)$ 就是$\pmb p^\prime$在$O_1$坐标系下的坐标。
注意到 $p,p^\prime,l,l^\prime$和基线$O_1O_2$都位于极平面之上。

有:
因此有:
利用叉乘的矩阵形式有:
由以上推导可知:
总结:
本质矩阵中包含 $R$ 和 $\pmb t$ (两个相机之间的旋转和平移关系),它通过空间中的物理点,联系了左右相机之间的位置关系。
2.2 基础矩阵(Fundamental Matrix)
若不是规范化摄像机该如何?这是就引入了基础矩阵
基础矩阵对一般的透视摄像机拍两个点图间极几何关系进行代数描述。