浅谈逻辑斯蒂回归模型

浅谈逻辑斯蒂回归模型

sigmod函数

​ $sigmod$函数及其导数形式如下：

$$f(x) = \frac{1}{1 + e^{-x}}$$ $$f^\prime (x)= f(x)*(1-f(x))$$

​ 逻辑斯蒂回归或者是$soft\max$回归，说是回归其实是在解决二分类或者多分类的问题。逻辑斯蒂模型如下：

$$y = \frac{1}{1 + e^{-（w^Tx +b)}}$$

​ 其中，$x \in R^n, w \in R^n$，$b$为偏置bias可以设置为0，$x$为样本的特征向量，$w$即要学习的参数。在给定一批有label的训练数据集后，我们可以根据极大似然估计或者梯度下降来得到最优的参数值，之后，给定某个测试数据，当：$y >= 0.5$，我们就把这个样本划为1类，否则就划为0类。

​ 其实，完整的二项逻辑斯蒂回归模型是定义如下的条件概率分布：

$$P(Y = 1|x) = \frac{\exp(w*x + b)}{1 + \exp(w*x + b)}$$ $$P(Y = 0|x) = \frac{1}{1 + \exp(w*x + b)}$$

​ 观察上述条件概率计算公式我们发现，当$wx+b > 0$的时候，$\exp(wx+b)>1,P(Y=1)$的概率一定高于$P(Y=0)$，我们就把其划分为1类。对于$P(Y=1)$的分布函数上下同除以分子$\exp$就得到了熟悉的逻辑斯蒂函数。

​ 事实上，逻辑斯蒂函数是在计算样本为1类的概率，由于是二分类，不是1类就是0类。

​ 本质上，逻辑斯蒂回归是一个线性分类器，以二维特征为例，如果不对特征进行任何组合，不使用核函数，其决策平面始终是一条直线：$w^Tx = 0$。

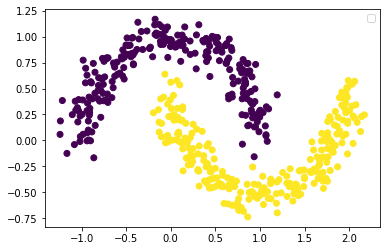
​ 以make moons生成的数据集为例，不对特征进行任何处理，决策平面如下：

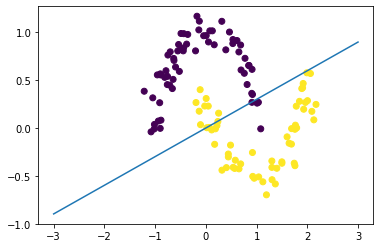
​ 若对两维特征进行平方处理，绘制的决策平面如下：

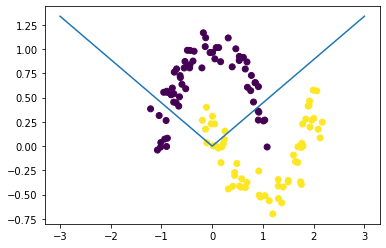
​ 谈到特征融合，决策树就可以拿来做特征融合（从根节点到叶子节点的每一条路径都是一个组合特征）。

softmax回归模型

参考：https://eli.thegreenplace.net/2016/the-softmax-function-and-its-derivative/

softmax函数

$$\sigma (\pmb x)_i = \frac{e^{x_i}}{\sum_j^n e^{x_j}},i = 1,...,n,\pmb x=(x_1,...,x_n)$$

定义：

$$S_j = \frac{e^{x_j}}{\sum_{k=1}^ne^{x_k}}, j = 1,2,...,n$$

​ 可以看到，softmax函数输入一个向量，输出是一个向量，是一个$\R^n \rightarrow \R^n$的函数。下面讨论其输入的各个分量的偏导，可以看到其输出分量对输入分量的偏导构成了一个$n \times n$的雅可比矩阵。

$$D_jS_i = \frac{\partial S_i}{\partial x_j}$$ $$DS = \begin{pmatrix}D_1S_1&D_1S_2&...&D_1S_n\\...&...&...&...\\D_nS_1&..&...&D_nS_n\end{pmatrix}$$

现在计算$D_jS_i$:

$$D_jS_i = \frac{\partial S_i}{\partial x_j} ,S_i =\frac{e^{x_i}}{\sum_{k=1}^ne^{x_k}}$$

$S_i$是个复合函数

$$S_i = \frac{g(x)}{h(x)},g(x) = e^{x_i},h(x)=\sum_{k=1}^ne^{x_k}$$

根据求导的除法法则：

$$D_jS_i = \frac{g^\prime(x)h(x)-h^\prime(x)g(x)}{h^2(x)}$$

这里需要分类讨论，即$i =j$和$i\not=j$的情况：$i=j$时，$g^\prime(x_j)=e^{x_j}=e^{x_i},h^\prime(x_i)=e^{x_i} = e^{x_j}$；否则$i\not=j$，$g^\prime(x_i)=0,h^\prime(x_i)=e^{x_j}$.

$i=j$时带入得：

$$D_jS_i = \frac{e^{x_i}\Sigma - e^{x_j}e^{x_i}}{\Sigma^2} = \frac{e^{x_i}}{\Sigma}\frac{\Sigma - e^{x_j}}{\Sigma} = S_i(1-S_j)$$

$i\not=j$时，带入得：

$$D_jS_i = \frac{0 - e^{x_i}e^{x_j}}{\Sigma^2} = -S_iS_j$$

综合以上讨论，有：

$$D_jS_i = S_i(\delta_{ij}-S_j)$$ $$i = j,\delta_{ij} = 1;i \not=j,\delta_{ij}=0$$

softmax回归模型

​ 值得注意的是，这里讲的softmax回归与softmax函数还是有一点不同的。softmax函数只是把给定的输入做了一个指数归一化；相比logistic回归模型的参数只是一个向量，softmax回归模型包含参数矩阵$W$，也就是每一个类别都对应一个n维向量，n为输入特征数量。

假设有$k$个类别，则权重矩阵：

$$W_{k \times n} = \begin{pmatrix}\pmb w_1^T\\...\\\pmb w_k^T\end{pmatrix}$$

输入为第$j$个类别的概率为：

$$P(y = j | \pmb x) = \frac{e^{\pmb x^T\pmb w_j}}{\sum_{i=1}^k e^{\pmb x^T\pmb w_i}}$$

模型针对给定输入预测类别的过程如下图所示：

注：T表示类别数量。

二者的关联

当$k = 2$的时候，

$$P(y = 1) = \frac{e^{\pmb x^T\pmb w_1}}{e^{\pmb x^T\pmb w_1} + e^{\pmb x^T\pmb w_0}} = \frac{e^{\pmb x^T(\pmb w_1 - \pmb w_0)}}{1 + e^{\pmb x^T(\pmb w_1 - \pmb w_0)}}$$ $$P(y = 0) = \frac{e^{\pmb x^T\pmb w_0}}{e^{\pmb x^T\pmb w_1} + e^{\pmb x^T\pmb w_0}} = \frac{1}{1 + e^{\pmb x^T(\pmb w_1 - \pmb w_0)}}$$

令$x^T(\pmb w_1 - \pmb w_0) = \pmb t$，那么：

$$P(y = 1) = \frac{e^{\pmb t}}{1 + e^{\pmb t}}$$ $$P(y = 0) = \frac{1}{1 + e^{\pmb t}}$$

我们可以发现，当类别数等于$2$时，softmax模型就会退化为logistic回归模型。