搜索

聚类

聚类

参考：《机器学习》，2016，周志华；统计学习方法，李航。

1. 聚类指标度量

如何衡量簇（类）与簇之间的距离？

  • 平均距离（average linkage）
  • 最大距离（complete linkage）
  • 最小距离（single linkage）
  • 中心距离

如何衡量聚类效果的好坏？

2. 原型聚类

2.1 K均值聚类

K均值聚类算法：

K均值算法的思想很简单，对于给定的样本集，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起（类内方差最小），而让簇间的距离尽量的大。注意到，采用到不同的距离可以得到不同的K均值聚类算法。最简单的就是使用欧氏距离，其他距离有： $Mahalanobis distance$，$L1 distance$等等。

给定包含有 $N$ 个样本的样本集 $D=\{\pmb x_1,\pmb x_2,…,\pmb x_N\}$ ，每个样本的维数为 $d$，即 $\pmb x_i \in \mathbb{R}^d$，K均值算法要将 $n$ 个样本划分为 $k$ 个类（簇）$C_1,C_2,…,C_k$，每一个类的中心（质心）可以用其均值向量表示：

$|C_k|$表示第$k$个簇中所包含的样本个数。注意到这是个虚拟点。

举个例子：$\pmb x_1 = (1,2,3)^T,\pmb x_2=(3,2,5)^T$，则：$\pmb \mu = (2,2,4)^T$。

这就是K均值算法的优化函数（目标函数），但是优化这个问题是个NP难问题，通常采用贪心迭代求解，直到$J$的变化小于某个阈值或者每个类的质心不在发生改变，算法结束。

算法描述：

  1. 随机选择k个样本点作为初始聚类中心，
  2. 对于每个样本，将其划分到距离最近的聚类中心的那个类中（聚类）
  3. 更新k个类的聚类中心
  4. 若聚类中心没有发生改变或者$J$收敛到某一阈值，算法结束，否则，执行2。

例子：

聚类例子

缺点：

  • 对初始化聚类中心敏感
  • K值难以指定
  • 只能收敛于局部极小
  • 对 outliers 噪声点敏感

注意：K-means与K近邻算法的区别

最大的区别K-means是无监督学习的聚类算法，没有样本输出；而K近邻是监督学习的分类算法，有对应的类别输出。K近邻基本不需要训练，对测试集里面的点，只需要找到在训练集中最近的k个点，用这最近的k个点的类别来决定测试点的类别。而K-means则有明显的训练过程，找到k个类别的最佳质心，从而决定样本的簇类别。

总结：

  1. K均值聚类基本思想，将数据划分为 $k$ 个类，同时最小化每个类的类内方差。可得目标函数：

  2. 优化目标函数，但是NP难问题，怎么近似求解？回答：a. 将所有样本点划分到距离最近的类中心对应的类（assignment step）；b. 更新类中心为类均值向量（refitting step）如此迭代。

  3. 但是以上过程能保证收敛吗？回答：可以。以上两个步骤都可以保证损失函数 $J$ 在每次迭代中都逐渐减小最后收敛，但不能保证一定收敛到全局极小值（可能收敛到局部极小）。证明略，可以自行谷歌。
  4. 本质上，k均值的迭代是一个运用EM算法的过程。

拓展1：当损失函数为：

即度量取为L1范数时，此时是什么聚类？

答：K中值聚类（K medians clustering）。很明显，此时向量 $\pmb \beta_k$已经不是均值向量了，而是中值向量。

拓展2：用另一种角度去看待K均值聚类

可知对于，每个样本$\pmb x_j$，都有 $k$ 个 $u$，且

这是含有等式约束的优化问题，且含有两组变量$\pmb \mu,u$，常用的办法是交替优化（固定一组，优化另一组）。

  • 当固定 $u$ 优化 $\pmb \mu$ 时，有：

得：

  • 当固定 $\pmb \mu_i$求 $u$ 得时候，

此时，各个簇的中心已经固定，要最小化 $J$，只需让每个样本划归到距离自己最近的类中心（贪心思想）即可（保证了所有样本和其所属类的中心之间的距离总和最小），对于样本$\pmb x_j$有：

$u\in\{0,1\}$，也就是说，每个样本只属于某个簇，明显是个硬划分聚类。

再回头看$\pmb \mu$更新公式，其实就是均值向量。

自己手动实现K均值聚类代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
from collections import defaultdict
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs

def eucli_distance(x, y):
    '''
        定义欧式距离
    '''
    return np.sqrt(np.sum((x - y)**2))

def assignment(points, centers):
    '''
        将所有像素点分至k个簇中
    '''
    assignments = []
    cnt = 0
    for p in points:
        # 找出与p距离最近的中心
        assignments.append(np.argmin([eucli_distance(p,c) for c in centers]))
    return assignments

def refitting(points, assignments):
    '''
        重新计算各个簇的均值
    '''
    clusters = defaultdict(list)
    means = []
    for (p,label) in zip(points, assignments):
        clusters[label].append(p)
    # 计算各个簇的均值
    for k in clusters:
        means.append(np.mean(clusters[k],0))
    return means

def kmeans(k, points, centers = None):
    # 每个像素点最终的聚类结果，k个类别
    # 初始化聚类中心
    if centers is None:
        centers = points[np.random.choice(len(points), k)]
    ite = 0
    while ite <= 100:
        labels = assignment(points, centers)
        centers = refitting(points, labels)
        ite += 1
        print(centers)
    return labels

if __name__ == "__main__":
    center=[[1,1],[-1,-1],[1,-1]]
	cluster_std=0.3
	X,_ = make_blobs(n_samples=200,centers=center,n_features=2,
                    cluster_std=cluster_std,random_state=0)
    res = kmeans(3,X)
    plt.scatter(X[:,0],X[:,1],c=res)
	plt.show()

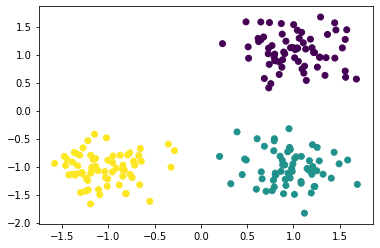
下面是在make_moons数据集上的聚类结果

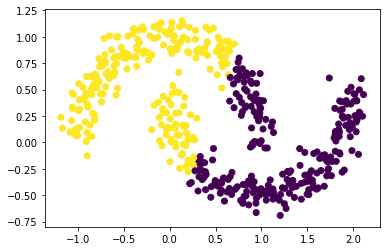
可以看到，K均值聚类的效果并不好。

图像分割

K均值做图像分割的思想非常简单。当输入是三通道图像时，每个像素点的三个通道值可以作为一个数据的特征，那么对于[width,height,3]的图像来说，共有width*height个数据点，每个点的特征维度是3维。K可以根据具体要求指定，当K为2时，即可用作前景、背景的分割。

在聚类完成后，对于每个像素点的聚类结果（属于哪个簇）分配不同的像素值然后reshape回原来的size即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
import cv2
img = cv2.imread('./3096.jpg').astype('float32')
# 彩色图像,rgb作为一个像素的特征，共有 width * height 个点，每个点的维度是3维的
data = img.reshape(-1,3)
#利用上述算法聚类 k = 2
res = kmeans(2,data)

r = np.array(res).reshape(256,-1)
for i in range(len(res)):
    if res[i] == 1:
        res[i] = 255 #为类别为1的簇分配白色像素
# 保存图像
cv2.imwrite("bin.jpg",r)

事实上，在K均值聚类中我们强制每一个样本只能属于一个类，通常这又被称为硬聚类。那有没有一种情况，某个样本可以属于多个类呢？这就涉及到了模糊聚类，模糊聚类引入了模糊簇和模糊集，允许一个样本属于多个簇。因此又被称为软聚类。关于聚类分析的更详细介绍，可以参见《数据挖掘概念与技术》（韩家炜等著），讲的非常好

K均值算法的过程可以被视为利用EM算法求解的过程，隐变量就是每个样本所属的类（簇）。

2.2 高斯混合聚类

高斯混合模型是基于概率模型的聚类，其基本思想就是用一个概率分布函数来表示每一个簇（类）。

3. 层次聚类

算法描述

  1. 构造n个类，每个类只包含一个样本
  2. 计算n个类之间的距离，得到$n \times n$的距离矩阵$D$
  3. 合并类间距离最小的两个类（注意：类间距离有不同的计算方式，可以根据情形来指定），形成一个新类。
  4. 计算新类与剩余类之间的距离，构造距离矩阵，若类别数等于k则算法结束，否则继续执行（3）。

4. 密度聚类

Density Based Spatial Clustering Applications with Noises（简称$\tt DBSCAN$）。

模型可视化：https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/

4.1 基本概念（白话版）

参数：$\epsilon$ （阈值），$min Points$（点数量）

核心对象：对于任一样本 $\pmb x\in D$，以 $\pmb x$ 为中心，半径为 $\epsilon$ 的圆内（领域）存在的其他样本数大于$min Points$，则 $\pmb x$ 为一个核心对象。（当然这里的“圆’指的是维数为2时，3维是球，更高维….反正就是与$\pmb x$距离小于$\epsilon$ 的）。

直接密度可达（密度直达）：对于核心对象点 $\pmb x_i$，若 $\pmb x_j$ 在以 $\pmb x_i$ 为中心的圆内，则称 $\pmb x_j$ 由 $\pmb x_i$ 密度直达。

密度可达： 若有一个样本序列，$\pmb x_0,\pmb x_1,…,\pmb x_k$，对任意$\pmb x_i, \pmb x_{i-1}$是密度直达的，则称从$\pmb x_0$ 到 $\pmb x_k$ 密度可达。

可以看出这条序列上的所有样本都是核心对象。这句话说的就是密度可达的传递性。图示：

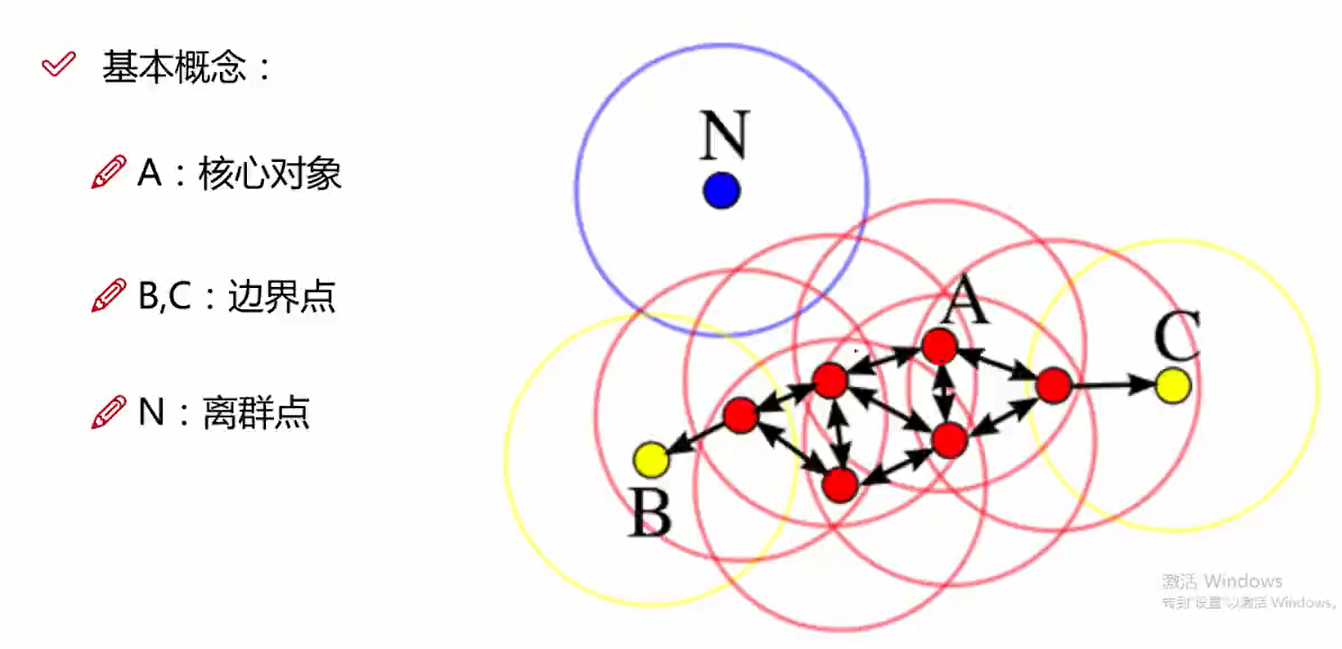
image-20201028200926586

上图中，红色的点都是密度直达的。$B、C$ 是密度相连的。

噪声点：从任何一个核心点都不密度可达。

4.2 算法描述

具体过程就像病毒的扩散过程一样，尽可能感染邻域内的点，当没有点可以感染，就再选一个没被感染的核心对象点继续感染，直到没有核心对象点了或者所有点都被感染了，算法停止。

输入：样本集$D=\{\pmb x_1,\pmb x_2,…,\pmb x_m\}$，领域参数$(\epsilon,min Points)$

输出：簇划分$C$

  1. 标记所有样本D为unvisited
  2. 遍历所有样本点，初始化每个样本的邻域信息若某个对象邻域内样本数量大于minPoints, 加入核心对象集合$\Gamma$。
  3. 从核心对象集合随机选取一个核心对象p：
    1. 创建一个核心对象队列$\Omega$，将$p$加入到其中
    2. 标记p为visited
    3. 创建一个簇C，将p添加到C中
    4. 当$\Omega$不为空：
      1. 取出一个核心对象
      2. 遍历其邻域集合：
        1. 若邻域内某样本q是核心对象
          1. 将q加入到$\Omega$，从$\Gamma$中删去q
        2. 否则如果 q 为unvisited：
          1. 标记q为visited
          2. 将q加入到C
    5. 输出C
  4. D中unvisited的为噪声点
  • 优势：
  1. 不需要指定簇的个数
  2. 擅长找到离群点
  3. 可以检测任意形状的簇
  • 缺点：
  1. 高维数据有些困难
  2. 参数难以选择

5. 均值漂移（Mean Shift）

入门参考：https://www.zhihu.com/question/67943169/answer/412092644

文献：Fukunaga K, Hostetler L. The estimation of the gradient of a density function, with applications in pattern recognition[J]. IEEE Transactions on information theory, 1975, 21(1): 32-40.（表示很难~）

代码：https://github.com/mattnedrich/MeanShift_py

上面这个代码用到了高斯核函数。

在不用核函数时，均值漂移其实就是选取一个样本，再设置一个窗口（bandwidth），然后计算窗口内所有样本的均值，该均值作为一个新的中心对象，再划一个窗口，如此迭代，直到最后收敛。拿二维数据来说，直观上均值会向数据集中的方向偏移。

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true