误差逆传播算法
给定如下结构的前馈全连接神经网络:
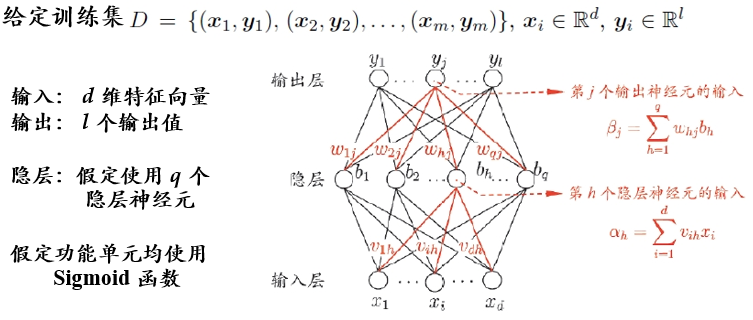
符号约定
输入样本 $\pmb x\in \mathbb{R}^d$,即神经网络输入层有 $d$ 个神经元。
输出 $\pmb y \in \mathbb{R}^l$,即神经网络输出层有 $l$ 个神经元。
输入层有 $q$ 个神经元,第 $h$ 个隐藏层神经元输入 $\alpha_h$,阈值 $\gamma_h$。输入层第 $i$ 个神经元到隐藏层第 $h$ 个神经元的权重 $v_{ih}$,第 $h$ 个隐藏层神经元输出为 $b_h$。
输出层有 $l$ 个神经元,第 $j$ 个神经元的输入 $\beta_j$,阈值为 $\theta_j$,隐藏层第 $h$ 个神经元到输出层第 $j$ 个神经元的权重为 $w_{hj}$, 第 $j$ 个输出层神经元的输出为 $\hat y_j$ 。
给定第 $k$ 个样本 $(\pmb x_k,\pmb y_k)$,神经网络输出为 $\hat {\pmb y_k}=(\hat y_1^k,\hat y_2^k,…,\hat y_l^k)$。
定义损失函数为均方误差函数,那么第 $k$ 个样本的损失为
假设 $f$ 为 $Sigmod$ 函数。
具体推导
- 隐藏层到输出层权重 $w_{hj}$ 的更新公式
根据网络结构图我们注意到有如下关系:
所以,根据链式求导法则,有:
现在就一步一步求三个偏导就好了。
首先求 $\frac{\partial E_k}{\partial \hat y_j^k}$。根据公式 $(5)$,有
接着求 $\frac{\partial \hat y_j^k}{\partial \beta_j}$。根据公式 $(4),(7)$有:
将公式 $(4)$ 带入 $(10)$中可得:
最后求 $\frac{\partial \beta_j}{\partial w_{hj}}$。根据公式 $(3)$,有:
综上,结合公式$(9),(11),(12)$,带入$ (8)$ 中,可得:
另外,我们定义 $g_j$ :
最后,隐藏层到输出层 $w_{hj}$ 的更新公式为:
其中,$\eta$ 为学习率。注意定义 $g_j$ 时已经取过负号了。
- 输入层到隐藏层权重 $v_{ih}$ 的更新公式
根据网络结构图,我们可知有如下关系:
因此,
根据公式 $(1),(2)$有
根据公式$(3),(14)$,有
综上,
另外,我们定义 $e_h$
最后,输入层到隐藏层权重 $v_{ih}$ 的更新公式为:
同样的,$\epsilon$ 为学习率。
- 阈值 $\theta_j$、$\gamma_h$ 的更新公式
注意到与 $w_{hj}$ 完全相同(仅仅是将$w_{hj}$换成了 $\theta_j$ ),所以有:
同理,
习题
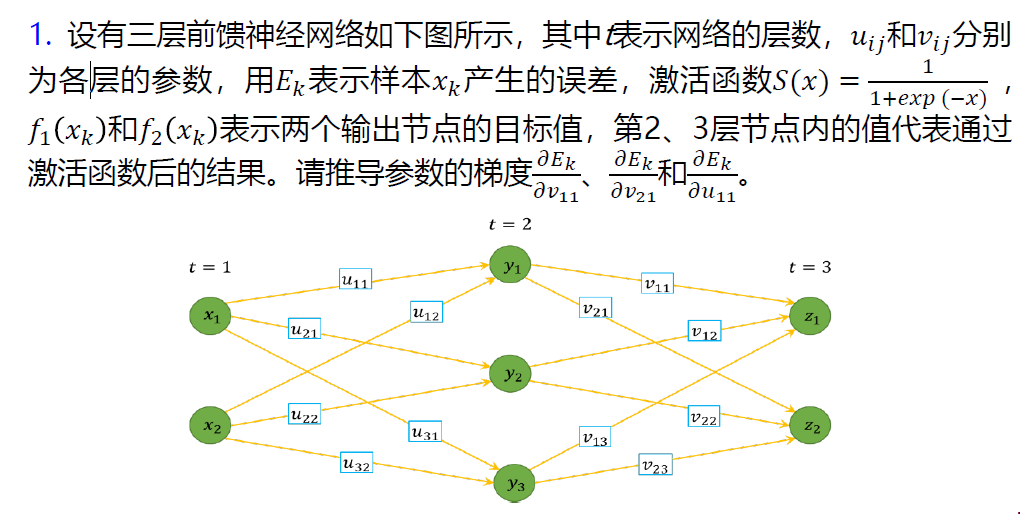
观察发现:
由此:
其中 $b_1$ 为隐藏层第一个神经元的输出。综上,有:
发现与公式$(14)$一致。
类似的,
观察$u_{11}$,有如下关系:
所以有:
带入可得:
其中,$w_{1j}$表示隐藏层第 $1$ 个神经元到输出层第 $j$ 个神经元的连接权重。
参考文献
周志华,机器学习