Graph Neutral Network和Graph Embedding
0. 概述
0.1 图的基础知识
通常定义一个图 $G=(V,E)$,其中 $V$为 顶点(Vertices)集合,$E$为边(Edges)集合。对于一条边$e=(u,v)$ 包含两个端点(Endpoints) u 和 v,同时 u 可以称为 v 的邻居(Neighbor)。当所有的边为有向边时,图称之为有向(Directed)图,当所有边为无向边时,图称之为无向(Undirected)图。在无向图中,对于一个顶点 v,令$d(v) $表示连接的边的数量,称之为度(Degree);有向图中又分为入度和出度。
对于一个无向图 $G=(V,E)$,其邻接矩阵(Adjacency Matrix)$A$通常定义为:
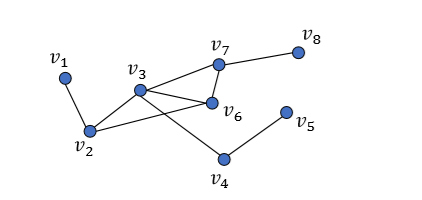
对于上面这个无向图,其度矩阵(degree matrix)如下。度矩阵$D$是一个对角矩阵。

图的拉普拉斯矩阵$L$定义为,在图论中,作为一个图的矩阵表示。拉普拉斯矩阵是对称的(Symmetric)。
另外一种更为常用的的是正则化的拉普拉斯矩阵(Symmetric normalized Laplacian)。
说明:$I$为单位矩阵;$D^{-\frac{1}{2}}$表示度矩阵对角线上的元素开平方根取倒数。
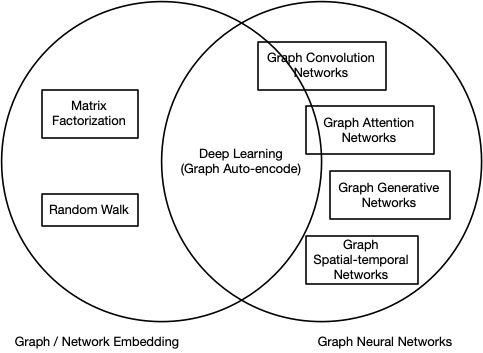
0.2 二者不同
图嵌入旨在通过保留图的网络拓扑结构和节点内容信息,将图中顶点表示为低维向量,以便使用简单的机器学习算法(例如,支持向量机分类)进行处理(摘自知乎:图神经网络(Graph Neural Networks)综述,作者:苏一。https://zhuanlan.zhihu.com/p/75307407)。
图神经网络是用于处理图数据(非欧式空间)的神经网络结构。
图嵌入和图神经网络的区别与联系。
1. Graph Embedding
Embedding在数学上是一个函数,将一个空间的点映射到另一个空间,通常是从高维抽象的空间映射到低维具象的空间,并且在低维空间保持原有的语义。早在2003年,Bengio就发表论文论述word embedding想法,将词汇映射到实数向量空间。而2013年google连发两篇论文推出word embedding的神经网咯工具包:skip-gram、cbow(连续词袋模型),使得embedding技术成为深度学习的基本操作,进而导致万物皆可embedding。
而基于图的embedding又可以分为基于顶点(vertex)和基于图(graph)。前者主要是将给定的图数据中的vertex表示为单独的向量(vector),后者将整个图进行embedding表示,之后可以进行图的分类等工作。下面分别介绍。
1.1 Vertex Embedding
1.1.1 DeepWalk
Perozzi B, Al-Rfou R, Skiena S. Deepwalk: Online learning of social representations[C]//Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. 2014: 701-710.

即:基于图上的随机游走进行节点采样,之后将采样到的节点集(每个节点feature使用one-hot表示或者随机向量)输入到skip-gram模型进行训练,得到节点的embedding。
1 | def RandomWalk(node,t): |
1.1.2 LINE
Tang J, Qu M, Wang M, et al. Line: Large-scale information network embedding[C]//Proceedings of the 24th international conference on world wide web. 2015: 1067-1077.
相似度定义
first-order proximity
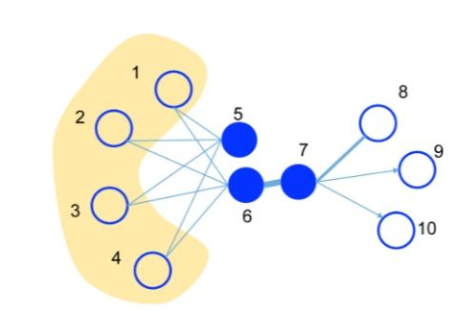
1阶相似度用于描述图中成对顶点之间的局部相似度,形式化描述为若$u,v$之间存在直连边,则边权$w_{uv}$即为两个顶点的相似度,若不存在直连边,则1阶相似度为0。 如上图,6和7之间存在直连边,且边权较大,则认为两者相似且1阶相似度较高,而5和6之间不存在直连边,则两者间1阶相似度为0。
second-order proximity
仅有1阶相似度就够了吗?显然不够,如上图,虽然5和6之间不存在直连边,但是他们有很多相同的邻居顶点(1,2,3,4),这其实也可以表明5和6是相似的,而2阶相似度就是用来描述这种关系的。 形式化定义为,令$p_u = (w_{u,1},…,w_{u,|V|})$ 表示顶点$u$与所有其他顶点间的1阶相似度,则 $u$ 与 $v$ 的2阶相似度可以通过 $p_{u}$ 和 $p_v$ 的相似度表示(两个顶点他们的邻居集合的相似程度)。若$u$与$v$之间不存在相同的邻居顶点,则2阶相似度为0。
目标函数
1st-order(用于无向图)
对于每条边集$E$中的任一条边$(i,j)$,邻接的两个节点$p_i,p_j$的联合分布定义为:
$u_i,u_j$即节点$v_i,v_j$的低维embedding表示。同时定义经验分布$\hat p$:
那么,目标函数就是尽可能地减小这两个分布的差异,衡量两个分布差异可以使用KL散度来衡量,进而:
2nd-order
当然也可以使用二者的结合。
1.1.3 Node2Vec
Grover A, Leskovec J. node2vec: Scalable feature learning for networks[C]//Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining. 2016: 855-864.
本质上也是基于随机游走,提出了一种新的节点采样策略,有“导向”的游走,即加入了参数来控制从某个节点到其他节点的概率。采样得到的节点集,仍使用word2vec形式进行训练。
如下图。p(return parameter)、q(in-out parameter)为超参数。
下图中,现处于节点v,上一个节点是t,那么从节点v到节点$t$、$x_1$、$x_2$、$x_3$的概率$\pi_{vx}$计算公式如下:
其中,$d_{tx}$表示上一节点和下一个能到达的节点的距离,$w_{vx}$即节点v与next节点连接边的权重(无向图中为1)。下图中,节点$t$与$x_1$直接有边相连接,$d$为1;$t$与$x_2$、$x_3$距离为2(不相邻);特别的,与上一个节点距离为0,概率为$\frac{1}{p}$。
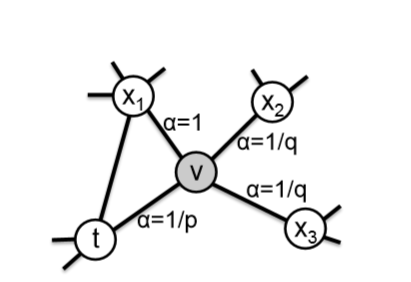
基于这种随机游走策略,使得该模型可以体现网络的同质性(homophily)或结构性(structural equivalence)。网络的“同质性”指距离相近的节点的embedding应尽量相似;“结构性”指的是结构上相似的节点的embedding应尽量相似。
为了能让graph embedding的结果能够表达网络的“结构性”,需要让游走的过程更倾向与BFS,因为BFS会更多的在当前节点的领域中游走遍历;为了表达”同质性”,则需要让游走过程倾向于DFS。
现在讨论超参数p、q,q越大,则随机游走到远方节点的可能性更大,随机游走策略就近似于DFS;反之,近似于BFS。
1.1.4 SDNE
Wang D, Cui P, Zhu W. Structural deep network embedding[C]//Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining. 2016: 1225-1234.
SDNE基于LINE研究的基础上,采用deep encoder-decoder模型进行embedding。
1.2 Graph Embedding
2. Graph Neural Network
图神经网络目前主要的任务包括:节点分类(node classification)、图分类(graph classification)、graph representation、link predication等等。
2.1 Neighborhood Aggravating
neighborhood aggravating即用节点的neighbor feature更新下一个的hidden state。
给定一张图,我们可以用与与节点邻接的节点集去表示该节点。下图中,A与B、C、D相邻接,而B又与A、C邻接等等,每个节点都可以使用与其相邻接的节点进行表示(aggravating)(每个节点都有一个初始状态【特征】,当前节点状态用其他节点的上一个状态【特征】表示)。通过其邻接节点聚合,这个节点就可以学到图的结构。
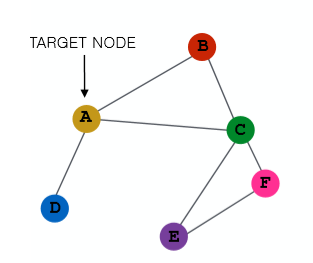

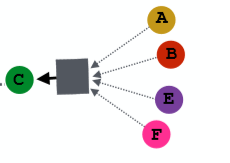
因此,我们可以定义任意层的网络来聚合各个节点的信息。(如下图,注:并非完整)
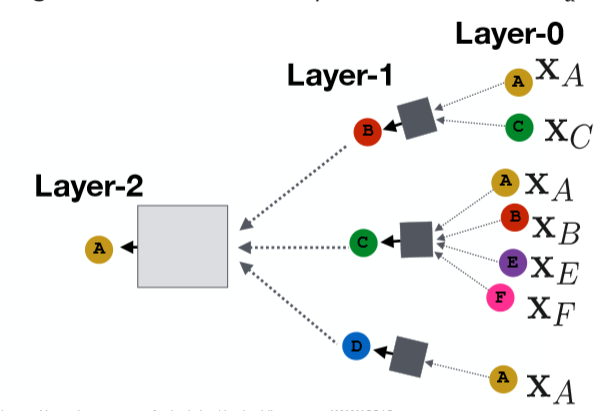
注:图中方块表示任意的聚合函数。
数学表示如下:
其中,k表示第k层(layer);v表示节点;$\sigma$表示激活函数;$h_u$表示节点$u$的状态;$N(v)$表示节点$v$的邻接节点集合;$|N(v)|$即邻接节点数量;$W、B$分别为权重矩阵和偏置(bias)。
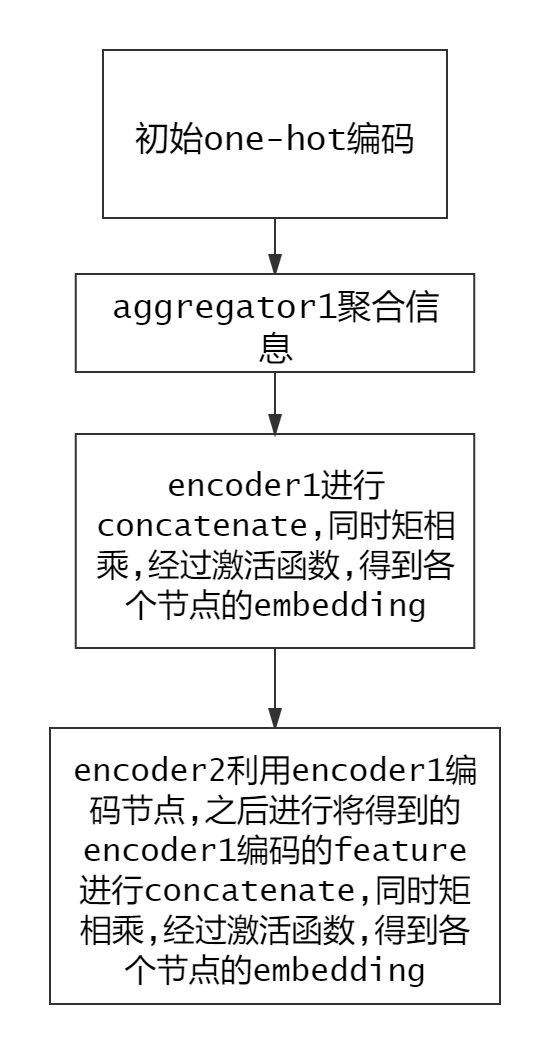
因此,我们只需定义一个聚合函数(sum、mean、max-pooling等),以及损失函数(比如:基于节点分类的交叉熵损失函数等),就可以开始迭代训练,最终得到各个节点的embedding向量。
2.2 Graph Convolution Networks
卷积网络大致分类如下图。
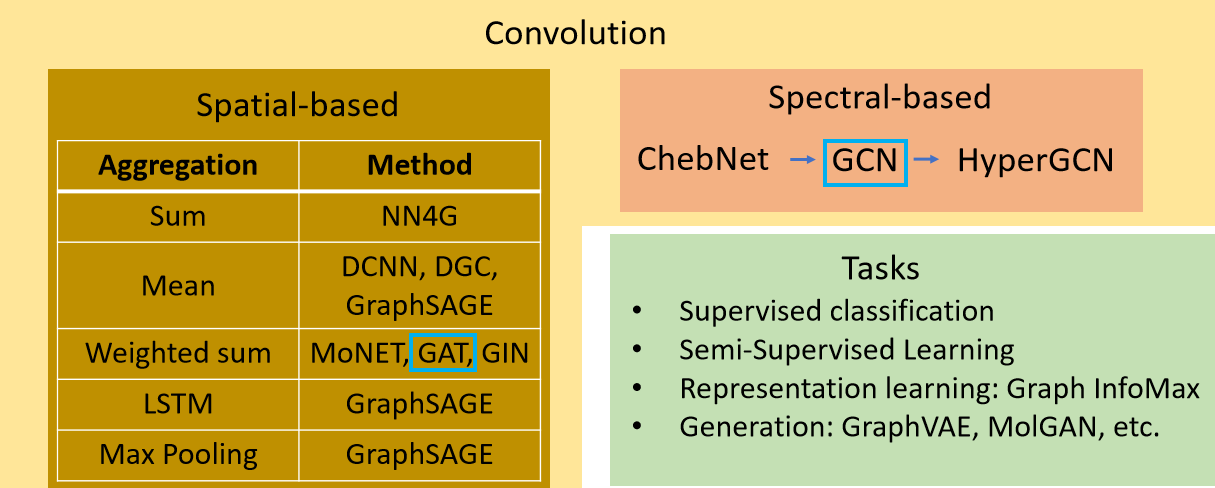
2.2.1 Spatial-based
空间卷积网络也是基于neighborhood aggravating的思想。
Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016.
这篇论文提出了著名的GCN模型,采用的图卷积网络在neighborhood aggravating上做出了一点改动。
矩阵形式如下:
其中$A$为图邻接矩阵,$D$为度矩阵,$I$为单位矩阵。
下面看一下具体的矩阵形式
1 | import numpy as np |
但是Kipf等人在他的论文中,对邻接矩阵$A$进行了标准化。即上文采用的公式。下面实现。
1 | # 定义图卷积 |
2.2.2 Spectral-based
谱图卷积网络基于图的信号处理,即图的拉普拉斯矩阵进行傅里叶变化(Fourier Transform)与逆变化(Inverse Fourier Transform),
图上的傅里叶变换
傅里叶变换可以将时域信号转为频域信号。时域即信号大小随时间而改变,其图像在二维平面中,横轴为时间,纵轴为信号大小,其图像是连续的;而频域图像,横轴代表频率大小,纵轴代表信号大小,其图像是离散的。频域图像本质上描述了一段信号中包含的具体成分(不同频率信号的叠加)如何。
而图上的傅里叶变换用到了图的拉普拉斯矩阵$L$,因为$L$是半正定矩阵,因此其特征值都非负。对其进行特征值分解有:
,其中$U$为特征向量,$\Lambda$为特征值矩阵,是一个对角矩阵,$\lambda_1,\lambda_2…$即特征值,且$\lambda_1<=\lambda_2<=…<=\lambda_n$。$\lambda$也代表了图上的频率。
下面直接给出图上傅里叶变换公式,具体推导略去。
给定图中某顶点$v$,其对应的信号(特征)为$x$,那么其傅里叶变换即:
可知$\hat x$为频域上信号,要重新换变换顶点域,就需要逆傅里叶变换即:
谱图卷积
要进行卷积,就需要在频域上进行卷积,即将顶点上的信号进行傅里叶变换后,定义对应的滤波器(滤波函数)$g_\theta(\lambda)$对其进行处理,再利用逆傅里叶变换还原为顶点域中。这里的滤波器或者说关于$\lambda$的滤波函数就是我们要通过训练学习的。说是关于$\lambda$的函数,就是说根据不同的$\lambda$给出不同的相应$\theta$。
由此,图上信号卷积即:
$f$即要学习的filter,$\otimes$即点积符号。因为最后$y$还是会和$U$运算,直接学习$U^Ty$并表示为:
,$g_{\theta}$是一个对角矩阵,就是要学习的参数。
但上面这样定义仍存在几个问题,一是当图太大时矩阵分解计算复杂度太高(a. 矩阵分解复杂度$O(n^3)$,b. 向量与矩阵相乘),二是这并非是局部的(localized)。进而又提出了ChebNet模型(Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering[C]. Advances in neural information processing systems. 2016: 3844-3852.)。
第一类切比雪夫多项式定义如下:
$\Lambda^k$表示对角矩阵的$k$次幂。
代码参考:https://github.com/dovelism/Traffic_Data_Projection_Using_GCN/
1 | class ChebConv(nn.Module): |
在推出ChebNet后,Kipf等人进一步将公式化简,推出一阶(k=1)ChebNet模型(Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016.),这就有了上面我们模型中采用的那个公式。
2.2 Graph Attention Networks
Veličković P, Cucurull G, Casanova A, et al. Graph attention networks[J]. arXiv preprint arXiv:1710.10903, 2017.
attention通俗的讲就是输入两个向量,然后输出一个分数;是一种思想,可以有不同的实现。
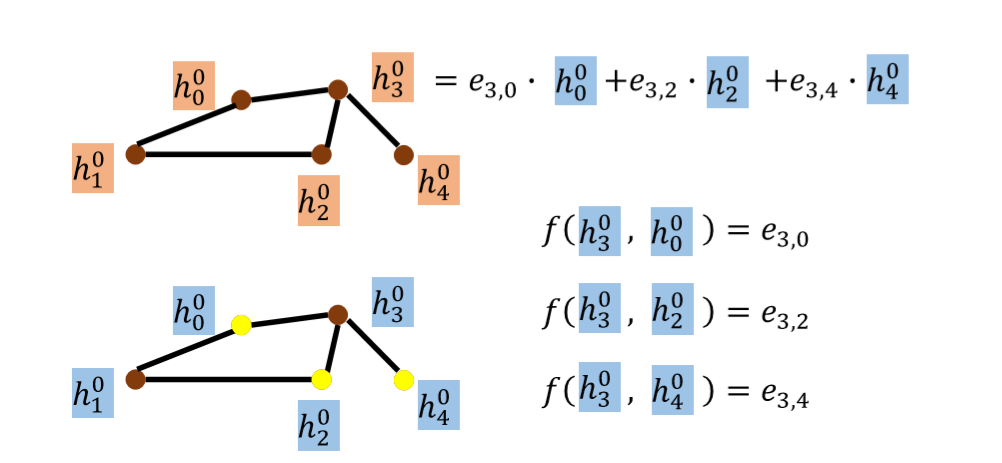
GAT在空间卷积的基础上,引入了注意力机制,注意力机制也赋予了模型一定的可解释性。加入了attention后,我们aggravating的时候就需要计算当前节点和邻接节点的权重,然后进行聚合。
节点v第k个状态更新公式如下:
其中$\alpha$就是计算得到的attention权重。
2.3 Graph SAGE
Hamilton W, Ying Z, Leskovec J. Inductive representation learning on large graphs[C]. Advances in neural information processing systems. 2017: 1024-1034.
SAGE即Sample and Aggregate。GCN(Kipf.2016)模型存在如下缺点:
- 对于静态图有效,当图结构发生改变(比如:节点的删除和更新)时,需重新训练模型。
- 当训练数据集非常时,内存无法全部加载图数据。
该篇论文提出了名为inductive learning的模型,能更好的适应动态图,同时针对新加入的节点也可以快速的生成node embedding。具体思想是不是去学习一个固定的embedding,而是学习一个聚合函数(aggregator),学习到的聚合函数需满足对称性(symmetry property),因为对称性确保了模型可以被训练而且可以应用于任意顺序的顶点邻居特征集合上。常见的聚合函数有:mean、lstm、pooling等。

可以看出模型针对每个节点每次聚合固定数量的邻居,而不必把所有数据加载到内存中。
K**是网络的层数,也代表着每个顶点能够聚合的邻接点的跳数,因为每增加一层,可以聚合更远的一层邻居的信息**。
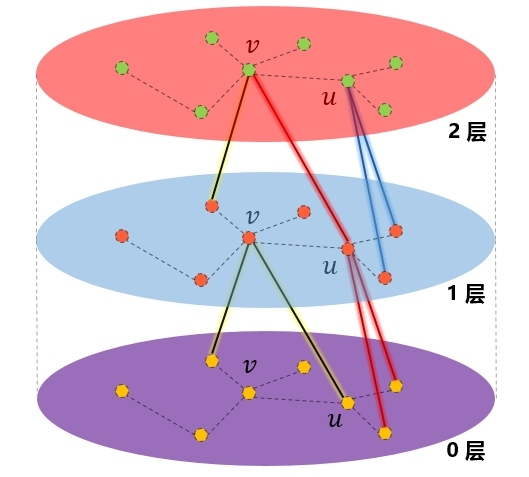
当新的节点加入到图中时,已经训练好的聚合函数(参数固定了)会聚合新节点的邻居然后生成该节点的embedding。
值得注意的是,当图中大量的节点有更新行为,图结构改变较大时,已经训练好的模型也需要重新训练,即模型退化为静态模型了。
参考资料:
李宏毅,深度学习
http://snap.stanford.edu/proj/embeddings-www/