PyTorch学习笔记之循环神经网络

2021-01-02

PyTorch学习笔记之循环神经网络

循环神经网络的提出是为了解决序列数据。如：翻译、语言识别、时间序列问题等。

1 基本结构

循环神经网络（Recurrent Neutral Network）不同于卷积网络，刚开始接触时个人感觉比较抽象。

在每个 cell 中，激活函数输入的不仅包含这个时序内输入的数据$x^{}$，而且还包括上个时序的输出 $a^{t-1}$(隐藏态)。因此，可以表示为：

$a^{\langle t \rangle} = g(W_{aa} a^{\langle t-1 \rangle} + W_{ax} x^{\langle t \rangle} + b_a)$

其中，$W_{aa}$表示 $t-1$ 时段输出的权重，$W_{ax}$表示 $t$ 时段输入的权重。之后，$a^{\langle t \rangle}$再向 $t+1$ 时段传播，或者经过$soft\max$函数，作为 $t$ 时段的输出。

基本RNN结构

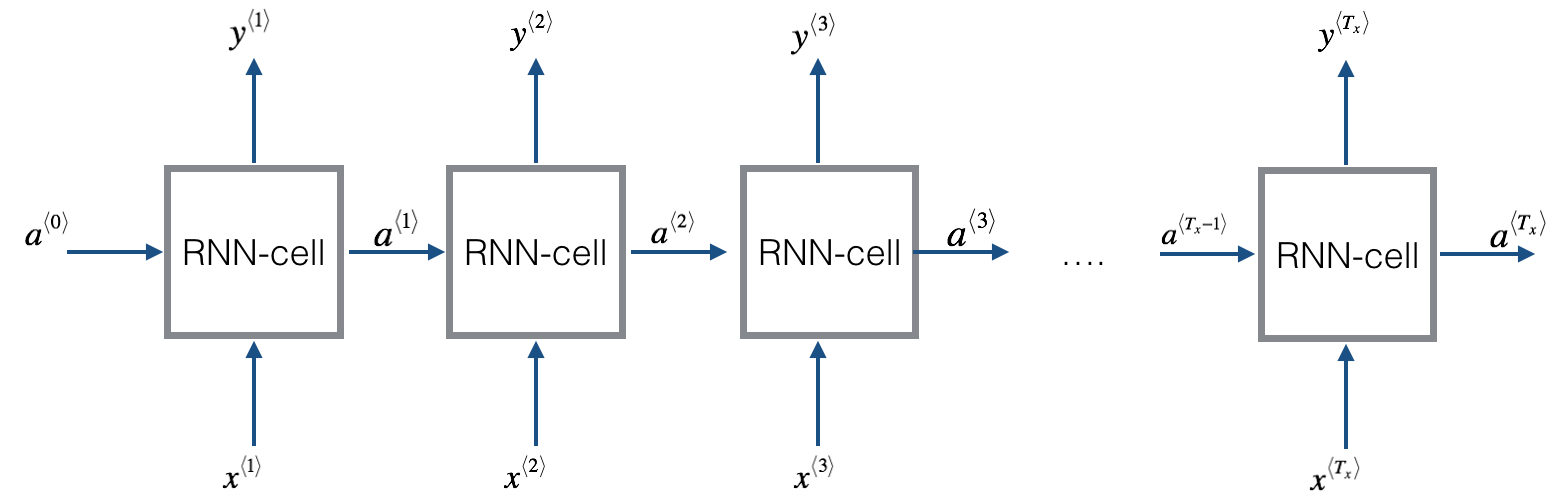
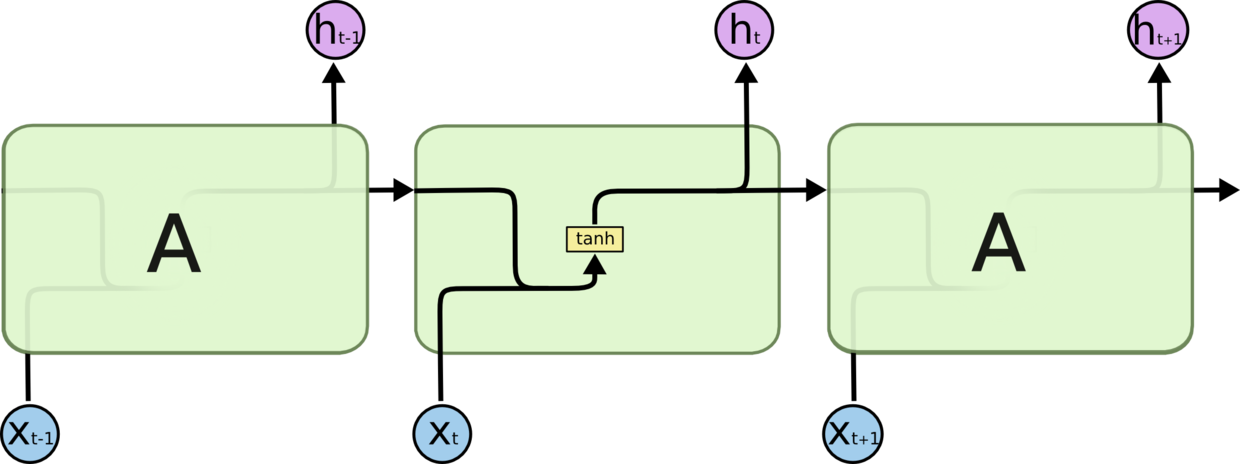
多层 RNN 结构：

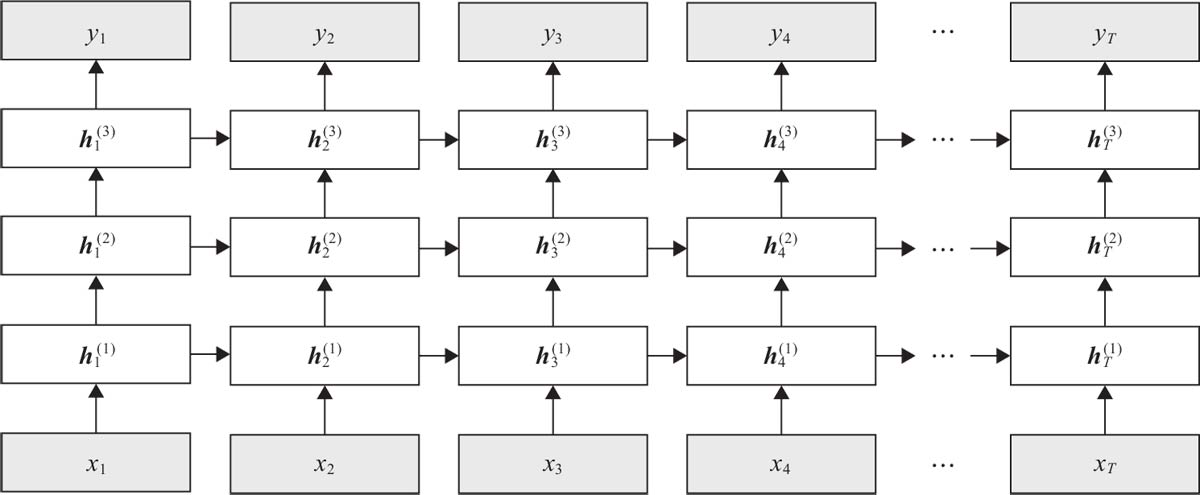
双向RNN结构

需要注意的是：前向和后向的隐藏态互不干扰和影响，每个时间步的输出由前向和后向的隐藏态共同决定。

RNN 的特点：

RNNs 主要用于处理序列数据。对于传统神经网络模型，从输入层到隐含层再到输出层，层与层之间一般为全连接，每层之间神经元是无连接的。但是传统神经网络无法处理数据间的前后关联问题。例如，为了预测句子的下一个单词，一般需要该词之前的语义信息。这是因为一个句子中前后单词是存在语义联系的。
RNNs 中当前单元的输出与之前步骤输出也有关，因此称之为循环神经网络。具体的表现形式为当前单元会对之前步骤信息进行储存并应用于当前输出的计算中。隐藏层之间的节点连接起来，隐藏层当前输出由当前时刻输入向量和之前时刻隐藏层状态共同决定。
标准的 RNNs 结构图，图中每个箭头代表做一次变换，也就是说箭头连接带有权值。
在标准的 RNN 结构中，隐层的神经元之间也是带有权值的，且权值共享。

2 LSTM 和 GRU

2.1 LSTM

三个门控：遗忘门、输入门、输出门

基本LSTM结构

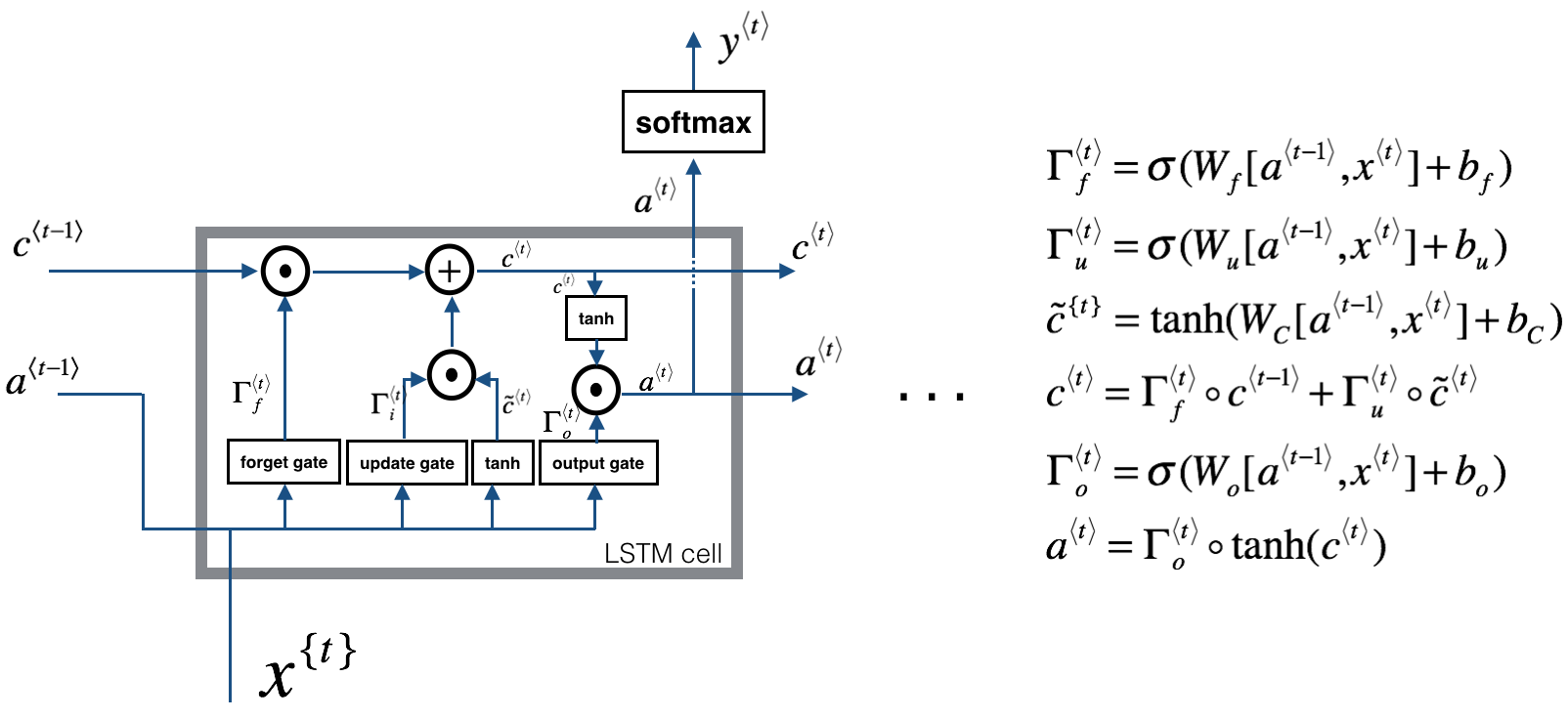
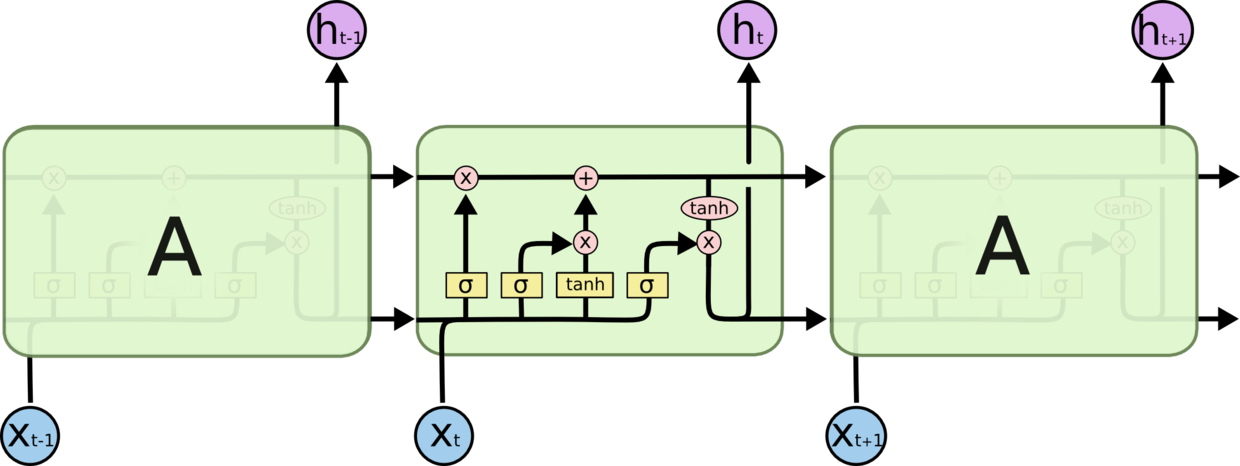
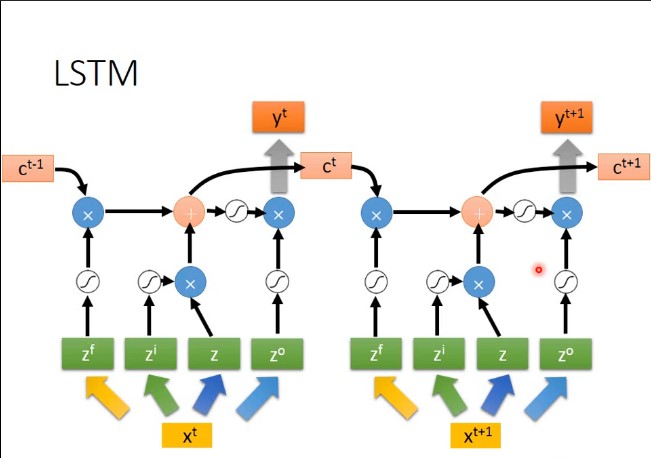
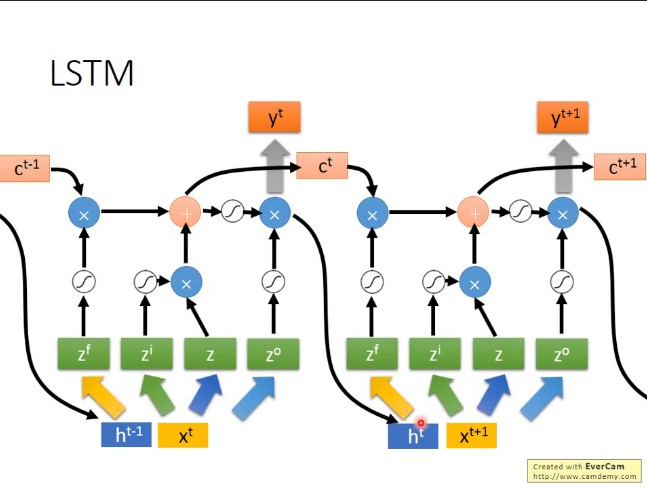
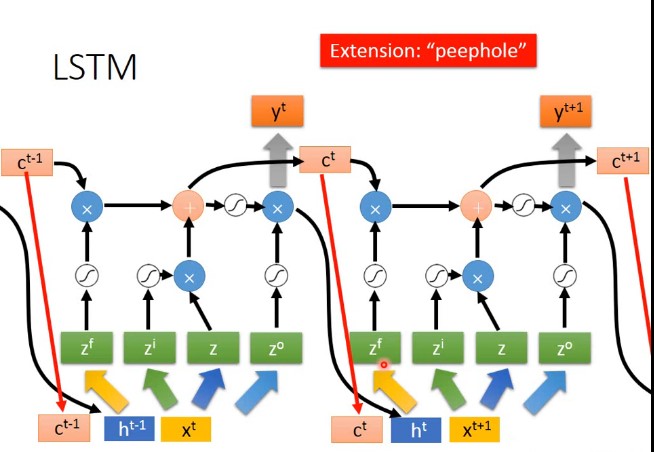
提出原因：

$RNN$ 在处理长期依赖（时间序列上距离较远的节点）时会遇到巨大的困难，因为计算距离较远的节点之间的联系时会涉及雅可比矩阵的多次相乘，会造成梯度消失或者梯度膨胀的现象。为了解决该问题，研究人员提出了许多解决办法，例如 ESN（Echo State Network），增加有漏单元（Leaky Units）等等。其中最成功应用最广泛的就是门限 RNN（Gated RNN），而 LSTM 就是门限 RNN 中最著名的一种。有漏单元通过设计连接间的权重系数，从而允许 RNN 累积距离较远节点间的长期联系；而门限 RNN 则泛化了这样的思想，允许在不同时刻改变该系数，且允许网络忘记当前已经累积的信息。

在torch.nn.LSTM中，返回两个值，一个是cell，一个是hidden。cell即记忆值，hidden即最后一个时间步的隐藏态。

2.2 GRU

提出原因

解决长距离梯度消失的问题

具体结构

两个门：update gate和reset gate

Update gate

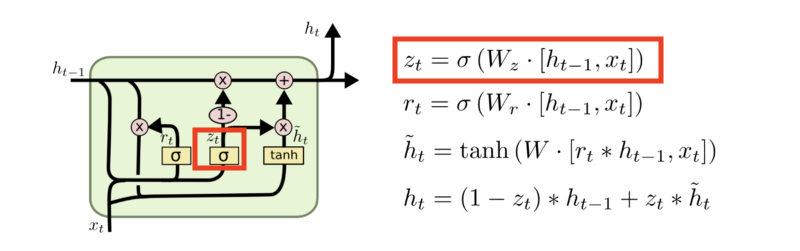
Reset gate

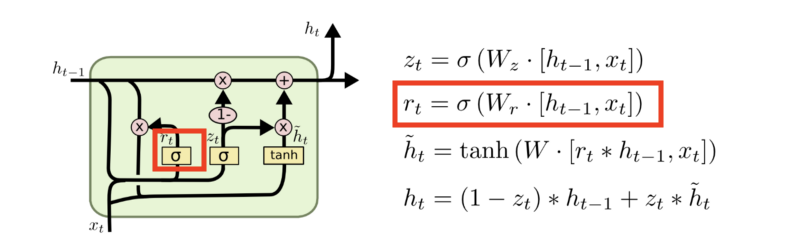
torch.nn.GRU 具体参数和nn.RNN类似

3 Pytorch 构建 RNN

$a^{\langle t \rangle} = g(W_{aa} a^{\langle t-1 \rangle} + W_{ax} x^{\langle t \rangle} + b_a)$

根据计算公式，为了提高运算速度，在具体实现经常采用矩阵相乘的形式。一般来说，可以分解为如下形式：

$\left[ \begin{matrix} a^{\langle t-1 \rangle} & x^{\langle t \rangle} \end{matrix} \right]* \left[ \begin{matrix} W_{aa} \\ W_{ax} \end{matrix} \right]$

即，将$W_{aa},W_{ax}$按照列进行拼接，将$a^{\langle t-1 \rangle},x^{\langle t \rangle}$ 按照行进行拼接。下面确定两个权重矩阵的维度。

如果假设输入($input$)的维度为 $x_m$，$hidden$ 的维度为$h_n$。可知$W_{aa},W_{ax}$ 的列维度一定是相同的，否则不能按$1*D$的大小，经过激活函数成为隐藏态，那么$D$的大小必然要和$hidden$的维度相同。因此$W_{aa},W_{ax}$的维度分别为：

$W_{aa} \rightarrow \left[h_n, h_n\right],W_{ax} \rightarrow [x_m, h_n]$

在Pytorch中，使用torch.nn.RNN来完成RNN的设计。

> import torch.nn as nn
> rnn = nn.RNN(input_size=5,hidden_size=10,num_layers=1)
> rnn.weight_hh_l0.shape #hidden to hidden 即W_aa
torch.Size([10, 10])
> rnn.weight_ih_l0.shape # input to hidden 即W_ax
torch.Size([10, 5])
> input = torch.randn(6,12,5) # 构造一个批次为10，input_dim为5,序列长度为6的矩阵，即每个序列长6，共有12个这样的序列，序列中每个时间步的dim为5
# input [src_len, batch, dim]
> output,hidden = rnn(input)
> output.shape
(torch.Size([6, 12, 10])
 #[src_len, batch, num_directions * hidden_size]

注意：在循环神经网络中，

$h_t = \tanh(w_{ih}x_t + b_{ih} + w_{hh}h_{t-1}+b_{hh})$

每个时间步都会输出一个hid向量，output就是所有hid向量形成的矩阵，而hidden向量是最后一个时间步产生的hid向量。将hid向量经过全连接或tanh等函数就会得到这个时间步的输出。

要构建双向循环神经网络，将bidirectional参数设为True即可。

> input = torch.randn(20,128,12) #[src_len, batch_size, embedded_dim]
> gru = nn.GRU(12, 512, bidirectional = True)
> outputs,hidden = gru(input)
> outputs.shape,hidden.shape
torch.Size([20, 128, 1024]),torch.Size([2, 128, 512])

输出维度解释：

output：[src len, batch size, hid dim * num directions]，注意第三个维度，因为是双向，因此从前向后会产生hidden，而从后向前也会产生hidden，即一个时间步由两个hidden产生，第三个维度就是[hid*2]。单向的话就是[hid*1]。

output[:,:,0]代表前向产生的hidden，output[:,:,1]代表后向产生的hidden。

hidden：[n layers * num directions, batch size, hid dim]。

hidden[0,:,:]所有前向产生的最后一个hidden向量，即到了序列的最后一个state，hidden[1,:,:]所有后向产生的第一个hidden向量，即到了序列的第一个state。

同nn.Conv2d不同的是，rnn的batch_size是第2个维度。

下面实际看一下：

> a = torch.randint(10,(2,3,4))# 假设这是hidden hid dim = 4, batch = 3, 前向3个hidden 
> a
tensor([[[0, 1, 7, 5],
         [8, 2, 5, 1],
         [5, 7, 8, 6]],

        [[2, 7, 7, 1],
         [1, 3, 8, 9],
         [7, 9, 4, 6]]])
> a[0,:,:] # 前向产生的hidden
tensor([[0, 1, 7, 5],
        [8, 2, 5, 1],
        [5, 7, 8, 6]])
> torch.cat((a[-2,:,:], a[-1,:,:]), dim = 1).shape
torch.Size([3, 8])
> torch.cat((a[-2,:,:], a[-1,:,:]), dim = 1)
# 即将每个句子的前向和后向合并成一个vector，经过合并后的hidden经过线性变换和激活函数可以传入decoder作为context向量或计算attention权重
tensor([[0, 1, 7, 5, 2, 7, 7, 1],
        [8, 2, 5, 1, 1, 3, 8, 9],
        [5, 7, 8, 6, 7, 9, 4, 6]])

attention权重生成的一种方式：

$weights = soft\max(W_1\tanh(W_2[h_{decoder\_hidden},h_{encoder\_hiddens}]))$

$W_1$、$W_2$可以是全连接层得到（nn.Linear）。

class Attention(nn.Module):
    def __init__(self, enc_hid_dim, dec_hid_dim):
        super().__init__()
        
        self.attn = nn.Linear((enc_hid_dim * 2) + dec_hid_dim, dec_hid_dim)
        self.v = nn.Linear(dec_hid_dim, 1, bias = False)
        
    def forward(self, hidden, encoder_outputs):
        
        #hidden = [batch size, dec hid dim]
        #encoder_outputs = [src len, batch size, enc hid dim * 2]
        
        batch_size = encoder_outputs.shape[1]
        src_len = encoder_outputs.shape[0]
        
        #repeat decoder hidden state src_len times
        hidden = hidden.unsqueeze(1).repeat(1, src_len, 1)
        
        encoder_outputs = encoder_outputs.permute(1, 0, 2)
        
        #hidden = [batch size, src len, dec hid dim]
        #encoder_outputs = [batch size, src len, enc hid dim * 2]
        
        energy = torch.tanh(self.attn(torch.cat((hidden, encoder_outputs), dim = 2))) 
        
        #energy = [batch size, src len, dec hid dim]

        attention = self.v(energy).squeeze(2)
        
        #attention= [batch size, src len]
        
        return F.softmax(attention, dim=1)
        #在每一行上进行softmax，即每一个单词的权重