机器视觉基础Lecture1

2021-01-02

机器视觉基础 Lecture 1

1. 卷积

卷积操作即用一个窗口在图像上滑动，图像上的像素与窗口内的数值相乘再相加，最后得到新的图像的过程；这个窗口也被称为滤波器/核。

卷积运算的性质：

交换律：$a b = b a$
结合律：$a (b c) = (a b) c$
分配律：$a(b + c) = ab + a*c$
数乘：$kab = a kb = k(a*b)$

可以看出，卷积运算是一种线性运算。

Question：

设计一个窗口，卷积过后图像保持不变

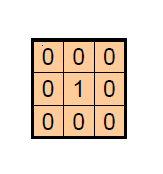
设计一个窗口，卷积过后图像向左平移1像素

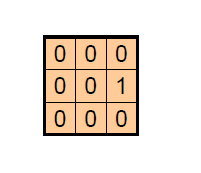
思考：为什么？对于每一个中心点像素，卷积过后更新为右边像素点像素值，整幅图卷积完就会向左平移。

设计一个窗口，卷积过后达到锐化（sharpen）的效果

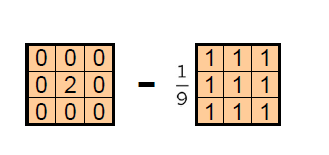
思考：为什么要这么设计？

步骤1：

步骤2：

综合步骤1、2可以看出，相当于将原来的像素值乘2再减去均值滤波平滑后的图像，就可以得到锐化后的图像。写成卷积核形式就是上述形式。

2. 各种滤波器

2.1 均值滤波

会出现“振零”现象。

2.2 高斯滤波

如何生成一个高斯滤波器？高斯函数（连续）：$G(x,y)=e^{-\frac{x^2+y^2}{\sigma^2}}$到卷积核（离散）。

matlab生成$\sigma=1$和$\sigma=3$的高斯核（归一化后的）：

0.0030    0.0133    0.0219    0.0133    0.0030
0.0133    0.0596    0.0983    0.0596    0.0133
0.0219    0.0983    0.1621    0.0983    0.0219
0.0133    0.0596    0.0983    0.0596    0.0133
0.0030    0.0133    0.0219    0.0133    0.0030

0.0318    0.0375    0.0397    0.0375    0.0318
0.0375    0.0443    0.0469    0.0443    0.0375
0.0397    0.0469    0.0495    0.0469    0.0397
0.0375    0.0443    0.0469    0.0443    0.0375
0.0318    0.0375    0.0397    0.0375    0.0318

一般设计的高斯滤波默认均值为0，并且根据“3$\sigma$原则”，窗口大小可以根据方差$\sigma$来设定，因此高斯滤波通常只指定一个参数：方差$\sigma$。

3$\sigma$原则：一维高斯函数我们可以发现，在以原点为中心，向左向右$3|\sigma|$距离内，函数积分可以达到$99.73\%$，也就是说$|x|>3\sigma$的点几乎约等于0，对卷积没有什么贡献。因此设计卷积核的时候。

窗口大小一定，方差$\sigma$对平滑效果的影响：$\sigma$越大，平滑效果越明显。

高斯函数的特点是：$\sigma$越小越集中（函数图像越尖，中心点的权值越大），这样加权平均自身权重更大，当$\sigma$逐渐增大，自身权重变小，加权过后自身信息丧失更加严重。

方差一定且在3$\sigma$原则下，窗口大小对平滑效果的影响：窗口越大，平滑效果越明显。

下面两张图展示了$\sigma=3$的情况下，窗口值大小为$3、9$的滤波结果。

窗口加大需要考虑的像素值越多自身信息丧失的也就越多。要求限定$3\sigma$原则原因是，超过这个范围，无论窗口多大平滑效果几乎一致（最外围差不多都是0了，对加权求和没有贡献）。

高斯噪声：采样于均值为0，方差为$\sigma$的高斯函数的值加到源图像上。

二维高斯函数（均值都是0）：

$G(x,y) = \frac{1}{ {2\pi\sigma^2}}e^{-\frac{x^2+y^2}{2\sigma^2}} = G(x)G(y)$ $G_x(x,y) = \frac{\partial G}{\partial x} =-\frac{1}{2\pi\sigma^2}\frac{x}{\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}$ $G_y(x,y)=\frac{\partial G}{\partial y} =-\frac{1}{2\pi\sigma^2}\frac{y}{\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}$ $G_{xx}(x,y) =-\frac{1}{2\pi\sigma^2}(\frac{1}{\sigma^2}-\frac{x^2}{\sigma^4})e^{-\frac{x^2+y^2}{2\sigma^2}}$ $G_{yy}(x,y) =-\frac{1}{2\pi\sigma^2}(\frac{1}{\sigma^2}-\frac{y^2}{\sigma^4})e^{-\frac{x^2+y^2}{2\sigma^2}}$

Laplacian of Gaussian (LoG)定义如下：

$LoG = \frac{\partial^2 G}{\partial x^2} + \frac{\partial^2 G}{\partial y^2} = G_{xx}(x,y) + G_{yy}(x,y) = \frac{1}{2\pi\sigma^2}\frac{x^2 + y^2-2\sigma^2}{\sigma^4}e^{-\frac{x^2+y^2}{2\sigma^2}}$

当用LoG核与图像做卷积会发现信号衰减，因此通常乘以$\sigma^2$ 做一下scale normaliz ation。

一个近似于该函数的离散卷积核($\sigma=1.4$)：

一维一阶高斯导数如下图所示（省略了系数$1/\sqrt{2\pi\sigma^2}$）：

1
2
3

x = np.linspace(-6,6,1000)
sigma_1 = 1.0
g_prime = -x/sigma_1**2 * np.exp(-x**2 / 2 / sigma_1 ** 2)

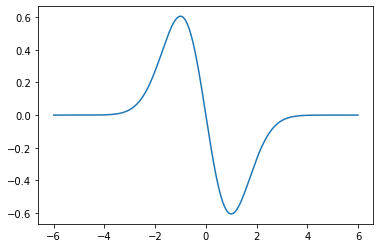
一维二阶高斯导数如下图所示：

.png)

将高斯函数离散化就可以得到高斯卷积核、一阶高斯卷积核。

在图像上，用高斯滤波就是取一个窗口，窗口内以中心点为（0,0）点然后给窗口内的不同坐标的窗口带入高斯函数中取值归一化后，在图像上滑动做卷积。

用高斯一阶导去和信号做卷积，干了两件事：一是平滑信号，二是求导。相当于先用高斯滤波平滑再求导。同理高斯二阶导 Laplacian of Gaussian，用高斯二阶导去和信号卷积。

高斯差分 DoG （Difference of Gaussian）相当于一个核（滤波器）。下图显示两个正态分布（均值都为1）的函数图像以及二者的差值图像，即DoG。参考：http://fourier.eng.hmc.edu/e161/lectures/gradient/node9.html

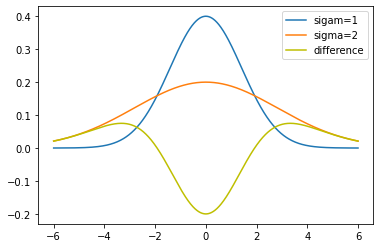
高斯核求和为1，用途：平滑
高斯一阶导核求和为0，用途：边缘提取

可以发现LoG与DoG的函数图像近似，因此为了提高计算效率（当 $\sigma$ 变大，模板尺寸随之也变大，计算开销增大）常用DoG核来替代LoG核（SIFT就是这么干的）。

2.3 中值滤波

中值滤波的窗口内没有权值，它的作用是把窗口内图像上所有像素值排序后取中值作为窗口中心点的像素值。

对椒盐噪声有效，是非线性滤波。

2.4 总结

高斯滤波以及均值滤波都可以起到平滑图像的作用，高斯滤波可以视为有权的均值滤波，图像在平滑的时候不仅会把噪声，也会把图像边缘信息平滑掉（噪声、边缘都是高频成分，因为像素值通常会发生剧烈变化），两者都是低通滤波（low-pass filter）。

而中值滤波能够保留边缘信息，是高通滤波（high-pass filter）。

3. 其他滤波

双边滤波（bilateral filter）、导向滤波（guided filter）、拉普拉斯滤波等。

拉普拉斯滤波（和LoG区分一下）：

$L(x,y) = \frac{\partial^2I}{\partial x^2} + \frac{\partial^2I}{\partial y^2}$

近似图像上二阶梯度的离散卷积核（拉普拉斯算子）：

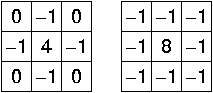
拉普拉斯滤波用途：边缘检测等。

经过拉普拉斯卷积后：

手动实现效果与cv2.Laplacian效果相同

kernel = np.array([[0,1,0],[1,-4,1],[0,1,0]])
# no padding 卷积
for i in range(1, img.shape[0] - 2):
    for j in range(1, img.shape[1] - 2):
        img[i,j] = np.sum(kernel * img[i:i+3, j:j+3])